Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ ( B B ' D ' D ) ⇒ B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
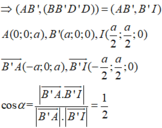

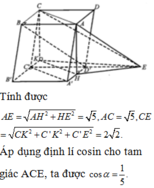
Ta có
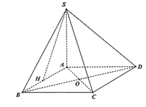
A H = 1 2 A B = a 2 ; S A = A B = a S H = H C = B H 2 + B C 2 = a 5 2
Do A H 2 + S A 2 = 5 a 2 4 = S H 2 nên S A ⊥ A B
Do đó S A ⊥ A B C D nên S C , A B C D ^ = S C A ^
Trong tam giác vuông SAC có tan α = tan S C A ^ = S A A C = 1 2
Đáp án A

Đáp án A
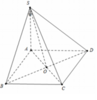
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .

Đáp án A.
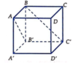
Đặt B ' 0 ; 0 ; 0 , A ' a ; 0 ; 0 , C ' 0 ; a ; 0 , B 0 ; 0 ; a ⇒ A a ; 0 ; a
Ta có B ' A → = a ; 0 ; a , B C ' → = 0 ; a ; − a , B ' B → = 0 ; 0 ; a
⇒ B ' A → , B C ' → = − a 2 ; a 2 ; a 2 ; B ' A → , B C ' → . B B ' → = a 3
d B ' A , B C ' = B ' A → , B C ' → . B B ' → B ' A → , B C ' → = a 3 3 a 4 = a 3 a 2 3 = a 3 3
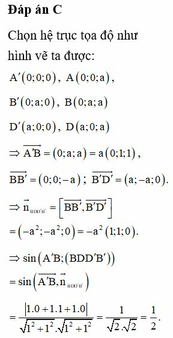
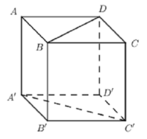





Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ B B ' D ' D
=> B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)