Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án C
Phương pháp:
- Gắn hệ trục tọa độ Oxyz, tìm tọa độ các điểm E, M.
- Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin α = n → . u → n → . u →
Cách giải:
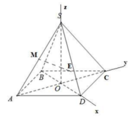
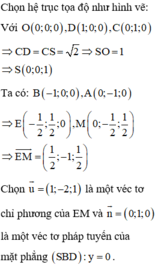
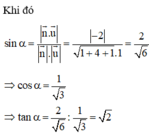

Đáp án A
Gọi I,J lần lượt là trung điểm cạnh BC và SA
Ta có A C ⊥ S B D , EI // AC, MJ//AC => E I ⊥ ( S B D ) , M J ⊥ ( S B D )
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
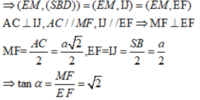
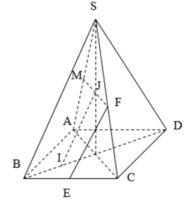

Đáp án A
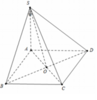
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .

Chọn C.
Phương pháp:
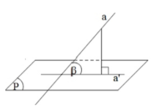
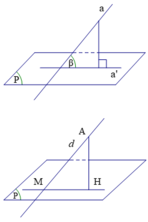
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
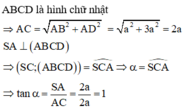

Nguyễn Thị Thu Hà thật là oai oai oai học giỏi mà bài tổng và hiệu cũng hỏi người khác
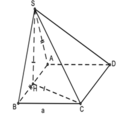
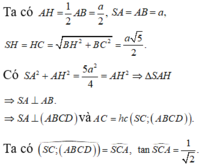



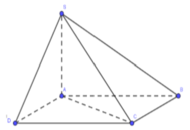
Ta có
A H = 1 2 A B = a 2 ; S A = A B = a S H = H C = B H 2 + B C 2 = a 5 2
Do A H 2 + S A 2 = 5 a 2 4 = S H 2 nên S A ⊥ A B
Do đó S A ⊥ A B C D nên S C , A B C D ^ = S C A ^
Trong tam giác vuông SAC có tan α = tan S C A ^ = S A A C = 1 2
Đáp án A