NH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 6 2019
15.
Ta có \(a+b+c+ab+bc+ac=6\)
Mà \(ab+bc+ac\le\left(a+b+c\right)^2\)
=> \(\left(a+b+c\right)^2+\left(a+b+c\right)-6\ge0\)
=> \(a+b+c\ge3\)
\(A=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2\ge3\)(ĐPCM)
17 tháng 6 2019
Bài 18, Đặt \(\left(a^2-bc;b^2-ca;c^2-ab\right)\rightarrow\left(x;y;z\right)\) thì bđt trở thành
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz\ge0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\ge0\)
\(\Leftrightarrow\frac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\ge0\)
Vì \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)nên ta đi chứng minh \(x+y+z\ge0\)
Thật vậy \(x+y+z=a^2-bc+b^2-ca+c^2-ab\)
\(=\frac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)(đúng)
Tóm lại bđt được chứng minh
Dấu "=": tại a=b=c
27 tháng 1 2022
Câu 1:
Sửa đề; BC=12cm
a: Xét ΔABD có \(\widehat{B}=\widehat{BAD}=60^0\)
nên ΔABD đều
=>BD=AB=6cm
=>BH=3cm
b: Ta có: BD+DC=BC
nên DC=BC-BD=12-6=6(cm)
Xét ΔDAC có DA=DC
nên ΔDAC cân tại D
c: Xét ΔABC có
AD là đường trung tuyến
AD=BC/2
Do đó: ΔABC vuông tại A
27 tháng 1 2022
Sửa đề; BC=12cm
a: Xét ΔABD có \(\widehat{B}=\widehat{BAD}=60^0\)
nên ΔABD đều
=>BD=AB=6cm
=>BH=3cm
b: Ta có: BD+DC=BC
nên DC=BC-BD=12-6=6(cm)
Xét ΔDAC có DA=DC
nên ΔDAC cân tại D
c: Xét ΔABC có
AD là đường trung tuyến
AD=BC/2
Do đó: ΔABC vuông tại A
27 tháng 1 2022
Câu 1:
Sửa đề; BC=12cm
a: Xét ΔABD có \(\widehat{B}=\widehat{BAD}=60^0\)
nên ΔABD đều
=>BD=AB=6cm
=>BH=3cm
b: Ta có: BD+DC=BC
nên DC=BC-BD=12-6=6(cm)
Xét ΔDAC có DA=DC
nên ΔDAC cân tại D
c: Xét ΔABC có
AD là đường trung tuyến
AD=BC/2
Do đó: ΔABC vuông tại A
25 tháng 1 2022
Bài 2:
a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó:ABEC là hình bình hành
Suy ra: AC=BE và AC//BE
b: Xét tứ giác AIEK có
AI//KE
AI=KE
Do đó: AIEK là hình bình hành
Suy ra: Hai đường chéo AE và IK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AE
nên M là trung điểm của IK
hay I,M,K thẳng hàng
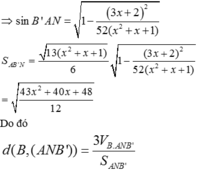
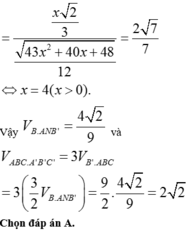
Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2