Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm của hình vuông
A D D ' A ' ⇒ A O ⊥ A ' B ' C D ⇒ d A , A ' B ' C D = A O = 2 a 2
Chọn đáp án D.

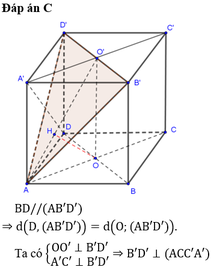
Đáp án C
Gọi I là trung điểm của BC, trong mặt phẳng (A′AI) kẻ AH vuông góc với A′I.
B C ⊥ A I B C ⊥ A A ' ⇒ B C ⊥ A H . A H ⊥ B C c m t A H ⊥ A ' I ⇒ A H ⊥ A ' B C .
Vậy d A , A ' B C = A H .
Ta có
1 A H 2 = 1 A A ' 2 + 1 A I 2 = 1 3 a 2 + 1 3 a 2 2 = 1 3 a 2 + 4 3 a 2 = 5 3 a 2 ⇒ A H = 15 a 5 .
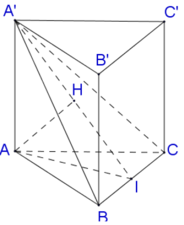

Chọn D.
Phương pháp : Sử dụng công thức tính thể tích ta có

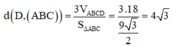

Mặt phẳng ( ABC ) có VTPT
n → = C A → , C B → = [ ( 1 ; 1 ; - 3 ) , ( 0 ; 3 ; - 3 ) ] = 3 2 ; 1 ; 1
Suy ra PT ( ABC ) : 2x + y + z -1 = 0
Dễ thấy I ∈ A B C nên khoảng cách từ D đến mặt phẳng (ABC) có giá trị lớn nhất bằng bán kính và bằng 3
Đáp án cần chọn là D



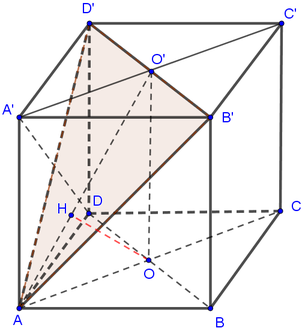

Đáp án A
Ta có: 1 d 2 = 1 A B 2 + 1 A A ' 2 = 2 a 2 ⇒ d = a 2 2 .