Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Gọi P là trung điểm cạnh BC
Tam giác MPN vuông tại P có
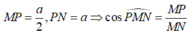
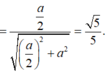
Chắc đề đúng là tính \(d\left(A;\left(BCC'B'\right)\right)\)
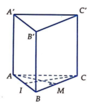
Gọi E là trung điểm BC \(\Rightarrow AE\perp BC\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AE\perp\left(BCC'B'\right)\)
\(\Rightarrow AE=d\left(A;\left(BCC'B'\right)\right)\)
Ta có: \(AE=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(\Rightarrow d\left(A;\left(BCC'B'\right)\right)=\dfrac{a\sqrt{3}}{2}\)
Đáp án B.
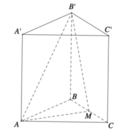
Gọi M là trung điểm của BC 
(ABC là tam giác đều)
(tam giác ABC đều)
(AM: gọi là đường vuông góc chung của 2 đường thẳng chéo nhau AA', BC).
Đáp án A
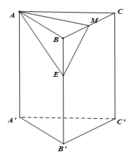
Gọi E là trung điểm của BB' => ME//B'C => (AME)//B'C
= d(C;(AME))
Vì 
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên :
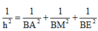
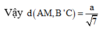
Đáp án D
Góc giữa B′C và mặt đáy (ABC) bằng 300 nên
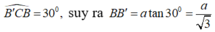
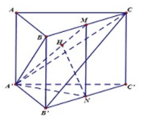
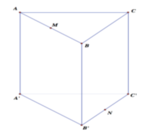
Gọi M,N lần lượt là trung điểm của BC,B′C′.
mà (A′BC) chứa A′C nên:
Kẻ NHvuông góc với AM, ta có
Ta có
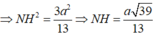
Vậy
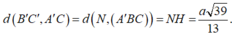
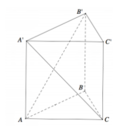
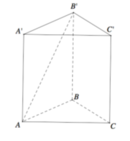
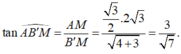
Đáp án B
Gọi I, M lần lượt là trung điểm AB′, BC
Do đó