

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



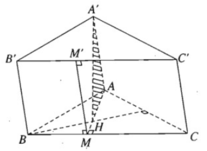
a) BC ⊥ AH và BC ⊥ A'H vì A'H ⊥ (ABC)
⇒ BC ⊥ (A'HA) ⇒ BC ⊥ AA'
Và B'C' ⊥ AA' vì BC // B'C'
b) Ta có AA' // BB' // CC' mà BC ⊥ AA' nên tứ giác BCC’B’ là hình chữ nhật. Vì AA' // (BCC'B') nên ta suy ra MM' ⊥ BC và MM' ⊥ B'C' hay MM’ là đường cao của hình chữ nhật BCC’B’.

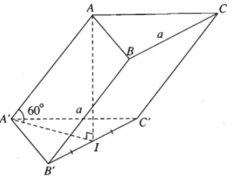
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
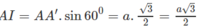
b) 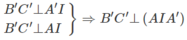
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.

a) Do MM' lần lượt là trung điểm của BC và B'C' nên M'M//BB'//CC'. Vì vậy MM'//AA'.
Vì vậy tứ giác A'M'MA là hình bình hành. Suy ra: AM//A'M'.
b) Trong mp (AA'M'M), ta có: MA' ∩ AM' = K.
Do \(K\in A'M\) và \(A'M\in\left(AB'C'\right)\) nên K (AB'C').
c) Có \(O=AB'\cap A'B\) nên \(O\in\left(AB'C'\right)\cap\left(BA'C'\right)\).
Suy ra: \(d\equiv CO'\).
d) Trong (AB'C'): C'O ∩ AM' = G vì vậy G ( AMM') . Mà O, M' lần lượt là trung điểm AB' và B'C' nên G là trọng tâm của tam giác AB'C'.

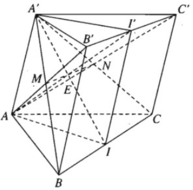
a) Ta có II′ // BB′ và II’ = BB’
Mặt khác AA′ // BB′ và AA’ = BB’ nên : AA′ // II′ và AA’ = II’
⇒ AA’II’ là hình bình hành.
⇒ AI // A′I′
b) Ta có:
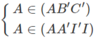
⇒ A ∈ (AB′C′) ∩ (AA′I′I)
Tương tự :
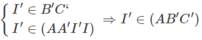
I′ ∈ (AB′C′) ∩ (AA′I′I) ⇒ (AB′C′) ∩ (AA′I′I) = AI′
Đặt AI′ ∩ A′I = E. Ta có:
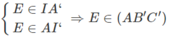
Vậy E là giao điểm của AI’ và mặt phẳng (AB’C’)
c) Ta có:
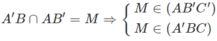
Tương tự:
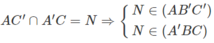
Vậy (AB′C′) ∩ (A′BC) = MN

Gọi D là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AD\perp BC\\AD=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
Gọi E là trung điểm BD \(\Rightarrow\) HE là đường trung bình tam giác ABD
\(\Rightarrow\left\{{}\begin{matrix}HE||AD\Rightarrow HE\perp BC\\HE=\dfrac{1}{2}AD=\dfrac{a\sqrt{3}}{4}\end{matrix}\right.\)
Mà \(B'H\perp\left(ABC\right)\Rightarrow B'H\perp BC\Rightarrow BC\perp\left(B'HE\right)\)
\(\Rightarrow\widehat{B'EH}\) là góc giữa (BCC'B') và đáy
\(\Rightarrow\widehat{B'HE}=60^0\)
\(\Rightarrow B'H=HE.tan60^0=\dfrac{3a}{4}\)
\(AA'||BB'\Rightarrow AA'||\left(BCC'B'\right)\Rightarrow d\left(AA';BC\right)=d\left(AA';\left(BCC'B'\right)\right)=d\left(A;\left(BCC'B'\right)\right)\)
Mà H là trung điểm AB \(\Rightarrow AB=2HB\Rightarrow d\left(A;\left(BCC'B'\right)\right)=2d\left(H;\left(BCC'B'\right)\right)\)
Từ H kẻ \(HK\perp B'E\)
Do \(BC\perp\left(B'HE\right)\Rightarrow\left(BCC'B'\right)\perp\left(B'HE\right)\)
Mà B'E là giao tuyến (B'HE) và (BCC'B')
\(\Rightarrow HK\perp\left(BCC'B'\right)\Rightarrow HK=d\left(H;\left(BCC'B'\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{B'H^2}+\dfrac{1}{HE^2}\Rightarrow HK=\dfrac{B'H.HE}{\sqrt{B'H^2+HE^2}}=\dfrac{3a}{8}\)
\(\Rightarrow d\left(AA';BC\right)=2HK=\dfrac{3a}{4}\)