Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
V A ' B ' C ' D ' . M N P Q V A ' B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' Q B ' B + D N D ' D = 7 2
Do đó thể tích khối đa diện nhỏ hơn là 15 2 V = 5 2 .2018 = 5045 6 .

Chọn A.
Phương pháp:
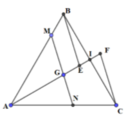
Cho tam giác đều ABC, G là trọng tâm tam giác ABC. Đường thẳng qua G cắt AB, AC lần lượt tại M, N. Khi đó, 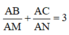
Thật vậy, gọi I là trung điểm của BC, qua B, C kẻ các đường thẳng song song MN, cắt đường thẳng AI tại E, F.

Cách giải:
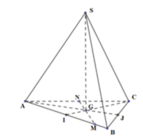
Do SABC là tứ diện đều, G là trọng tâm tam giác ABC

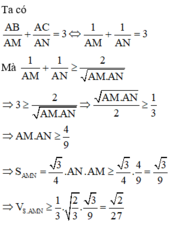


Phương pháp:
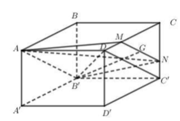
- Dựng mặt phẳng chứa B'G và song song với C'D.
- Xác định khối đa diện và tính thể tích bằng cách cộng trừ thể tích các khối đa diện đơn giản.
Cách giải:

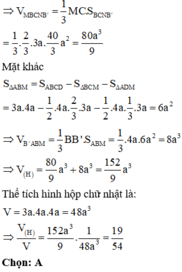







Đáp án D
Phương pháp: Sử dụng phương pháp tọa độ hóa.
Cách giải:
Gắn hệ trục Oxyz, có các tia Ox, Oy, Oz lần lượt trùng với các tia AB, AD, AA’.
A(0;0;0), B(1;0;0), C(1;2;0), D(0;2;0), A’(0;0;3), B’(1;0;3), C’(1;2;3), D’(0;2;3)
(P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Gọi E(a;0;0), F(0;b;0), G(0;0;c), (a,b,c > 0)
Phương trình mặt phẳng (P): x a + y b + c z = 1
Thể tích tứ diện AEFG: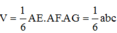
Ta có: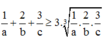

=>Vmin = 27 khi và chỉ khi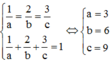
Khi đó, T = AE + AF + AG = a + b + c = 3 + 6 + 9 = 18