Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)

1:
a: BC vuông góc BA
BC vuông góc SA
=>BC vuông góc (SAB)
b: Kẻ BK vuông góc AC, BH vuông góc SK
=>BH=d(B;(SAC))
\(AC=\sqrt{BA^2+BC^2}=5a\)
AK=(4a)^2/5a=3,2a
BK=4a*3a/5a=2,4a
\(SB=\sqrt{2a^2+16a^2}=3a\sqrt{2}\)
SK=căn 2a^2+10,24a^2=a*3căn 34/5
BK=2,4a
SK^2+BK^2=SB^2
nên ΔSKB vuông tại K
=>K trùng với H
=>d(B;(SAC))=BK=2,4a

\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\)
Mà \(AC\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
Do \(SO\perp\left(ABCD\right)\Rightarrow OC\) là hình chiếu của SC lên (ABCD)
\(\Rightarrow\widehat{SCO}\) là góc giữa cạnh bên và đáy \(\Rightarrow\widehat{SCO}=60^0\)
\(AC=a\sqrt{2}\Rightarrow OC=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
\(\Rightarrow SO=OC.tan60^0=\frac{a\sqrt{6}}{2}\)
Gọi M là trung điểm CD \(\Rightarrow OM\perp CD\Rightarrow CD\perp\left(SOM\right)\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy
\(OM=\frac{1}{2}BC=\frac{a}{2}\Rightarrow tan\widehat{SMO}=\frac{SO}{OM}=\sqrt{6}\)
\(\Rightarrow\widehat{SMO}\approx67^047'\)
Từ O kẻ \(OH\perp SM\Rightarrow OH\perp\left(SCD\right)\Rightarrow OH=d\left(O;\left(SCD\right)\right)\)
\(\frac{1}{OH^2}=\frac{1}{SO^2}+\frac{1}{OM^2}\Rightarrow OH=\frac{SO.OM}{\sqrt{SO^2+OM^2}}=\frac{a\sqrt{42}}{14}\)
\(AC=2OC\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=\frac{a\sqrt{42}}{7}\)

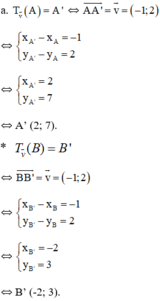
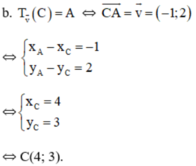
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

a) giải cách này để bn dể hình dung nha :)
ta có : 2 người \(A;F\) ngồi cạnh nhau thì ta cứ tưởng tượng như lấy sợi dây buột 2 người này lại .
\(\Rightarrow\) ta có số cách để xếp \(A;F\) trên 6 vị trí là : \(2.\left(6-1\right)=10\)
và số cách xếp \(4\) người còn lại trên \(4\) vị trí còn lại là : \(A^4_4=4!=24\)
\(\Rightarrow\) số cách sắp xếp sao cho \(A\) và \(F\) ngồi cạnh nhau là \(10.24=240\) cách
b) ta có số cách sắp xếp \(6\) người ngồi trên \(6\) vị trí là \(A^6_6=6!=720\) cách
\(\Rightarrow\) số cách sắp xếp sao cho \(A\) và \(F\) không ngồi cạnh nhau là : \(720-240=480\) cách
vậy .....................................................................................................................
Đáp án A