Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

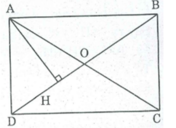
Ta có:
DB = HD + HB = 2 + 6 = 8 (cm)
AC = DB (tính chất hình chữ nhật)
OA = OB = OC = OD = 1/2 BD = 4 (cm)
OD = OH + HD
⇒ OH = OD – HD = 4 – 2 = 2 (cm)
Suy ra: OH = HD = 2 cm nên H là trung điểm của OD
Tam giác ADO có AH là đường cao đồng thời là đường trung tuyến nên tam giác ADO cân tại A
⇒AD = AO = 4 (cm)
Trong tam giác vuông ABD có ∠ (BAD) = 90 0
B D 2 = A B 2 + A D 2 (định lý Pi-ta-go) ⇒ A B 2 = B D 2 - A D 2
AB = B D 2 - A D 2 = 8 2 - 4 2 ≈ 7 (cm).

BD = HD + HB
= 2 + 6
= 8 ( cm )
ABCD là hình chữ nhật
=> OA = OB = OC = OD = \(\frac{BD}{2}=\frac{AC}{2}=\frac{8}{2}=4\) \(\left(cm\right)\)
=> OH = OD – HD
= 4 - 2 = 2 ( cm )
\(\Delta AOD\)cân => AO = AD = 4 ( cm )
AD định lý py ta go cho tam giác ABD
BD2 = AB2 + AD2
=> AB2 = 82 - 42 = 64 - 16 = 48
=> \(AB\approx7\left(cm\right)\)
Kẻ đường chéo AC cắt BD tại O
Ta có: BD = DH + HB = 2 + 6 = 8 (cm)
\(AC=BD\Rightarrow OA=OB=OC=OD=\frac{BD}{2}=\frac{8}{2}=4\left(cm\right)\)
\(\Rightarrow OH=OD-HD=4-2=2\left(cm\right)\Rightarrow OH=HD\left(=2cm\right)\)
=> AH là đường trung tuyến của t/g OAD
Mà AH là đường cao của t/g OAD
=> t/g OAD cân tại A => OA = AD = 4 (cm)
Xét t/g ABD vuông tại A có: \(AB^2+AD^2=BD^2\) (định lí pytago)
\(\Rightarrow AB=\sqrt{BD^2-AD^2}=\sqrt{8^2-4^2}=\sqrt{48}\approx7\left(cm\right)\)

a) Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
hay BD=10(cm)
b) Xét ΔDHA vuông tại H và ΔDAB vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔDHA\(\sim\)ΔDAB(g-g)

hình bạn tự vẽ nha
áp dụng định lý py ta go vào tam giác ABD ta có AD^2 + AB^2 =64 (1)
áp dụng định lý pytago vào tam giác ABH ta có AB^2 = AH^2+ 36 (2)
áp dụng định lý pytago vào tam giác AHD ta có AD^2= AH^2 +4 (3)
thay (2)và (3) vào (1)
ta có 2AH^2 =24
=> AH^2 =12
thay AH^2=12 lần lượt vào 2 và 3
=> AB^2=12+36=48=>AB=\(\sqrt{48}\)
AD^2=12+4=16 => AD=4