Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`Answer:`

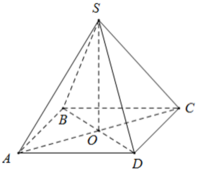
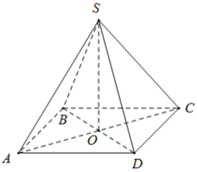
Gọi `H` là trung điểm của `CD`
\(\Rightarrow SH\perp CD\)
\(OH=\frac{1}{2}AD=\frac{1}{2}.10=5cm\)
Ta có: \(SO=12cm\)
\(\Rightarrow SH=\sqrt{SO^2+OH^2}=\sqrt{5^2+12^2}=\sqrt{169}=13cm\)
\(\Rightarrow S_{\Delta SCD}=\frac{1}{2}.SH.CD=\frac{1}{2}.13.10=65cm^2\)
\(\Rightarrow S_{xungquanh}=S_{\Delta SCD}.4=65.4=260cm^2\)

a) Áp dụng định lý Pytago, ta được:
AC2=AB2+BC2=2AB2AC2=AB2+BC2=2AB2
⇒AC=AB√2=10√2cm⇒AC=AB2=102cm
b) Gọi MM là trung điểm ABAB
⇒MA=MB=MO=5cm⇒MA=MB=MO=5cm
⇒SM⊥AB⇒SM⊥AB (ΔSAB∆SAB cân tại SS)
⇒SM=√SA2−AM2=√122−52=√119cm⇒SM=SA2−AM2=122−52=119cm
⇒SO=√SM2−OM2=√119−52=√94cm⇒SO=SM2−OM2=119−52=94cm
⇒VS.ABCD=13.SABCD.SO=13.AB2.SO=102.943=94003cm3

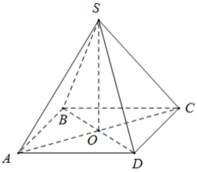
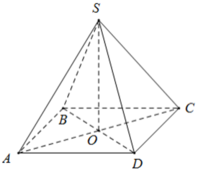
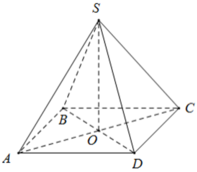
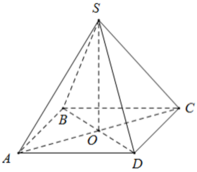
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
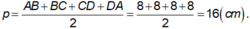
+ BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 ).
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )


a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
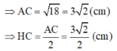
Lại có: SH2 = SC2 - HC2 (Pytago)
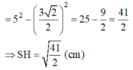
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
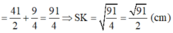
![]()
![]()
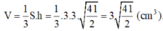
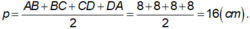

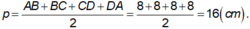

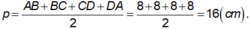

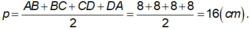

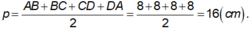

\(V_{ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.12.10^2=400\left(cm^3\right)\)
Gọi \(H\)là hình chiếu vuông góc \(S\)đến \(AB\).
\(SH^2=SO^2+OH^2=12^2+5^2=13^2\Rightarrow SH=13\left(cm\right)\)
\(S_{xq}=4.S_{SAB}=4.\frac{1}{2}.13.10=260\left(cm^2\right)\)