Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
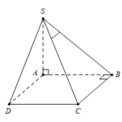
Vì 2 mp S A B , S A D vuông góc với đáy ⇒ S A ⊥ A B C D
Và ABCD là hình vuông ⇒ A B ⊥ B C ⇒ B C ⊥ m p S A B
Khi đó S C ; S A B ⏜ = S C ; S B ⏜ = B S C ⏜ = α ∈ 0 ° ; 90 °
Tam giác SBC vuông tại B, có tan B S C ⏜ = B C S B = a : a 2 = 1 2
Vậy tan α = 1 2

Đáp án C
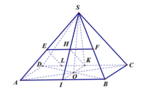
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:
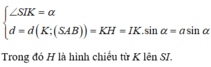

Đáp án A.
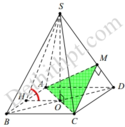
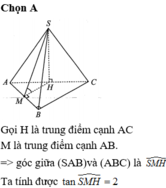
Gọi O là tâm hình vuông ABCD, H là trung điểm AB.
⇒ A B ⊥ S H O ⇒ S A B ; A B C D ^ = S H ; O H ^ = S H O ^ = α . ⇒ c o s α = 1 3 ⇒ tan α = 3 x 2 − 1 = 2 2 ⇒ S O = tan α × O H = a 2 .
Kẻ CM vuông góc với SD M ∈ S D ⇒ m p P ≡ m p A C M .
Mặt phẳng A M C chia khối chóp A.ABCD thành hai khối đa diện gồm M.ACD có thể tích là V 1 và khối đa diện còn lại có thể tích V 2 .
Diện tích tam giác SAB là S Δ S A B = 1 2 . S H . A B = a 2 . 3 a 2 = 3 a 2 4 .
Và
S D = S O 2 + D O 2 = a 10 2 ⇒ S Δ . S C D = 1 2 . S H . S D ⇒ C M = 3 a 10 .
Tam giác MCD vuông tại M ⇒ M D = C D 2 − M C 2 = a 10 ⇒ M D S D = 1 5 .
Ta có:
V M . A C D V S . A C D = M D S D = 1 5 ⇒ V M . A C D = V S . A B C D 10 ⇔ V 1 = V 1 + V 2 10 ⇔ V 1 V 2 = 1 9 .

Chọn C.
Phương pháp:
Thể tích của khối chóp ngoại tiếp hình chóp

Cách giải:
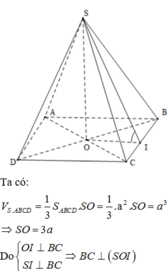
Gọi O là tâm của hình vuông ABCD, I là trung điểm của BC.




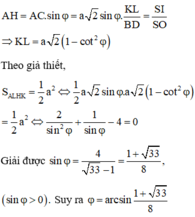
Đáp án C.
Gọi O là tâm đáy, ta kẻ O H ⊥ A B Có A B ⊥ S O ; A B ⊥ O H ⇒ A B ⊥ S O H ⇒ S K ⊥ A B .
Vậy góc giữa 2 mp S A B và A B C D là góc S H O ^ .
Có O H = a 2 ; S H = a 2 − a 2 2 = 3 2 . a ⇒ cos S H O ^ = O H S H = 1 3