Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
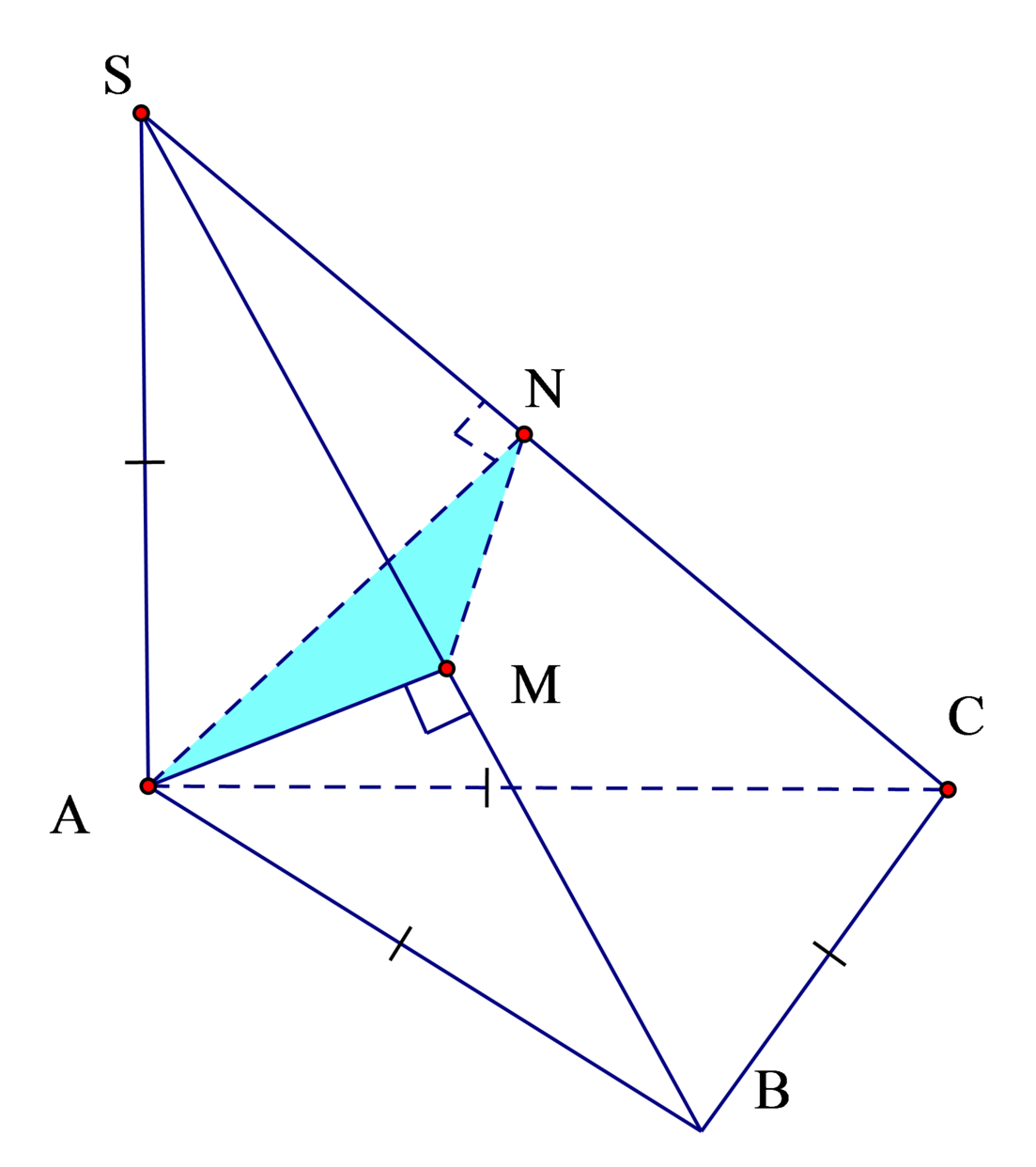
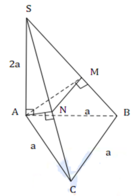
Do Δ S A B , Δ S A C cân nên M, N là trung điểm SB, SC
Ta có: V S . A M N V S . A B C = S M S B S N S C = 1 2 1 2 = 1 4 ⇒ V A . B C M N V S . A B C = 3 4
⇒ V A . B C M N = 3 4 V S . A B C = 1 4 S A . d t A B C = 1 4 a . a 2 3 4 = a 3 3 16

Gọi N là trung điểm của BC, dựng hình bình hành ABNP.
Ta có:
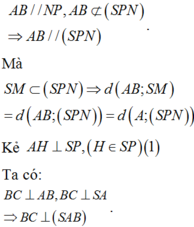
Mà
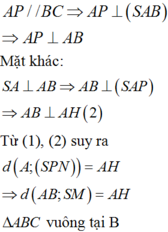
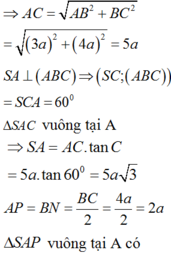
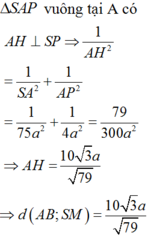
Chọn: B

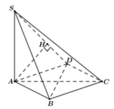
Xác định được ![]()
Khi đó ta tính được ![]()
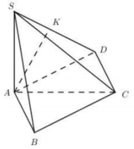
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
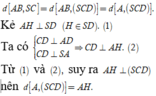
Xét tam giác vuông SAD có 
Chọn C.

Đáp án A.
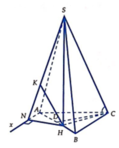
Ta có S C H ^ = 60 ° và
H C = a 7 3 ; S H = H C tan S C H ^ = a 21 3
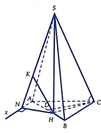
Từ A kẻ tia A x / / C B (như hình vẽ). Khi đó B C / / S A x và do B A = 3 2 H A nên
d B C , S A = d B C , S A x = d B , S A x = 3 2 d H , S A x
Gọi N và K lần lượt là hình chiếu vuông góc của H trên Ax và SN.
Do A N ⊥ S H N và H K ⊥ S N nên H K ⊥ S A N . Khi đó d B C , S A = 3 2 H K .
Ta có
A H = 2 a 3 ; H N = A H sin N A H ^ = a 3 3 .
Suy ra H K = H N . H S H N 2 + H S 2 = a 42 12 . Vậy d B C , S A = a 42 8 .

Đáp án A.
Phương pháp:
- Phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng trong không gian:
d Δ 1 ; Δ 2 = M 1 M 2 → . u 1 → ; u 2 → u 1 → ; u 2 → , M 1 ∈ Δ 1 ; M 2 ∈ Δ 2
Cách giải:
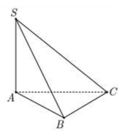
Gắn hệ trục tọa độ (như hình vẽ):
A 0 ; 0 ; 0 , B 0 ; a ; 0 , C a 3 2 ; a 2 ; 0 , S 0 ; 0 ; 3 a
M, N lần lượt là trung điểm của AB, SC
⇒ M 0 ; a 2 ; 0 , N a 3 4 ; a 4 ; 3 a 2
⇒ A N → = a 3 4 ; a 4 ; 3 a 2 ; C M → = − a 3 2 ; 0 ; 0
Đường thẳng AN có 1 VTCP u 1 → = 3 ; 1 ; 6 ,
đi qua điểm A 0 ; 0 ; 0 .
Đường thẳng CM có 1 VTCP u 1 → = 1 ; 0 ; 0 , đi qua điểm A 0 ; a 2 ; 0 .
A M → = 0 ; a 2 ; 0 , u 1 → ; u 2 → = 0 ; 6 ; − 1
d A N ; C M = A M → . u 1 → ; u 2 → u 1 → ; u 2 → = 0.0 + a 2 .6 + 0. − 1 0 2 + 6 2 + 1 2 = 3 a 37
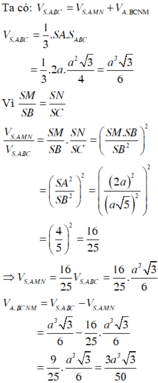



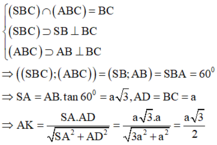
Đáp án D
Phương pháp giải: Dựng hình, dựa vào tam giác cân để xác định các yếu tố vuông góc
Lời giải: Với hình chóp tam giác đều S.ABC thì: góc giữa các cạnh bên và mặt đáy bằng nhau, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trọng tâm tam giác ABC, hai cạnh đối diện vuông góc với nhau.