Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
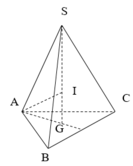
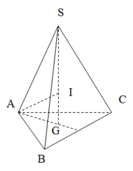
Gọi I là tâm mặt cầu ngoại tiếp hình chóp
I G = x ⇒ S I = 3 - x A I 2 = x 2 + 1 3 = 3 - x 2 = S I 2 ⇔ x = 4 3 3 ⇒ A I 2 = R 2 = 25 27 S = 4 πR 2 = 100 π 27

Đáp án A
Gọi H là trọng tâm tam giác ABC suy ra SH = h; SA = b
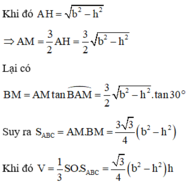

Đáp án A.
Ta có m .3 x 2 − 7 x + 12 − 1 + 3 2 x − x 2 = 9.3 10 − 5 x + m ⇔ m . 3 x 2 − 7 x + 12 − 1 = 3 12 − 5 x − 3 2 x − x 2 .
⇔ m . 3 x 2 − 7 x + 12 − 1 = 3 2 x − x 2 3 x 2 − 7 x + 12 − 1 ⇔ 3 x 2 − 7 x + 12 − 1 3 2 x − x 2 − m = 0
⇔ 3 x 2 − 7 x + 12 = 1 3 2 x − x 2 − m = 0 ⇔ x 2 − 7 x + 12 = 0 2 x − x 2 = log 3 m ⇔ x = 4 ; x = 3 2 x − x 2 = log 3 m *
Để phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi
(*) có nghiệm duy nhất khác 4 ; 3 .
(*) có hai ngiệm phân biệt, 1 nghiệm bằng 4, nghiệm còn lại khác 3.
(*) có hai nghiệm phân biệt, 1 nghiệm bằng 3, nghiệm còn lại khác 4.
Vậy có 3 giá trị m cần tìm.

Xét hình chóp S.ABC có đáy ABC là tam giác đều cạnh ![]()
Thể tích khối chóp 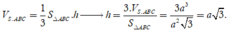
Chọn A.

Chọn C
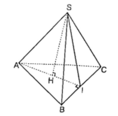
Phương pháp:

Cách giải:
Hình chóp tam giác đều ABC có chiều cao a, cạnh bên 2a.
Gọi H là trọng tâm tam giác ABC => SH là đường cao hình chóp => SH = a
Gọi I là trung điểm BC
Do tam giác ABC đều


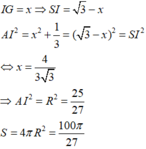
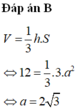
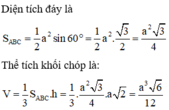
Đáp án C