Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{V_{SAHKE}}{V_{SABCD}}=\dfrac{2V_{SAHK}}{2V_{SABC}}=\dfrac{V_{SAHK}}{V_{SABC}}\)
\(V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.BC=\dfrac{a^3}{3}\); \(V_{SABCD}=\dfrac{2a^3}{3}\)
\(\dfrac{SH}{SB}=\dfrac{SA^2}{SB}:SB=\left(\dfrac{SA}{SB}\right)^2\); \(\dfrac{SK}{SC}=\dfrac{SA^2}{SC}:SC=\left(\dfrac{SA}{SC}\right)^2\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{6}\)
\(\dfrac{V_{SAHK}}{V_{SABC}}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAHKE}=\left(\dfrac{2a}{a\sqrt{5}}\right)^2.\left(\dfrac{2a}{a\sqrt{6}}\right)^2.\dfrac{2a^3}{3}=\dfrac{16a^3}{45}\)

Đáp án A
Phương pháp:
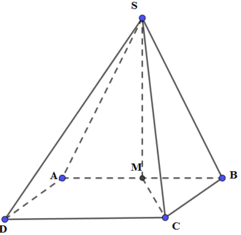
+) Xác định góc giữa SC và mặt đáy là góc giữa SC và hình chiếu của nó trên (ABCD).
+) Áp dụng định lí Pytago tính SM.
![]()
Cách giải:
Gọi M là trung điểm của AB ⇒ SM ⊥ (ABCD)


Do H là trung điểm của AB,
=> SH vuông (ABCD)
Do đó SH vuông HD. Có \(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
\(\Rightarrow V_{S.ABCD}=\frac{1}{3}S.H.S_{ABCD}=\frac{a^3}{3}\)
Gọi K là hình chiếu vuông góc với H trên BD vs2 E là là hình chiếu vuông góc của H trên SK.
Có : BD vuông HK, BD vuông SH, BD vuông (SHK)
=> BD vuông HE.
Mà HE vuông SK
Do đó HE vuông (SBD)
Ta có : HK = HB \(\sin\widehat{KBH}=\frac{a\sqrt{2}}{4}\)
=> HE = \(\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{4}{3}\)
Do đó, d (A,(SBD)) = 2d (H,(SBD)) = 2HE = 2a/3
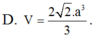
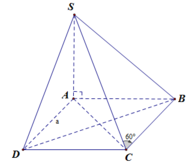

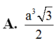

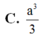
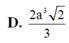
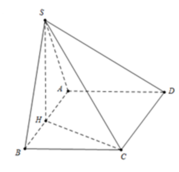
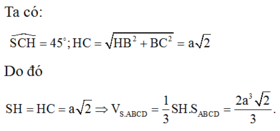
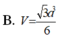
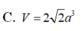
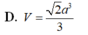
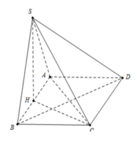
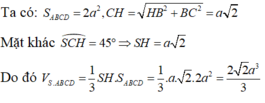
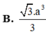
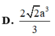

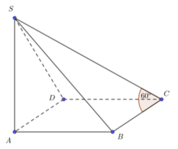

gọi H là h/c cua S lên (ABCD)
HC=3/4 AC\(\Rightarrow\)SH
S\(_{ABCD}\)=
V\(SABCD\)=\(\frac{1}{3}\)SH.S\(_{ABCD}\)