Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

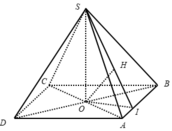
- Gọi O là giao điểm của AC và BD.
- Kẻ: OI ⊥ AB, OH ⊥ SI.
+) Ta có:
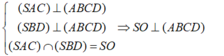
+) Ta lại có:
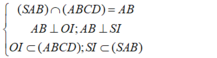
- Do đó, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng góc 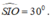
+) Khi đó: CD // AB nên CD // ( SAB).
Suy ra:

- Ta có:
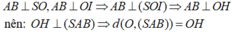
+) Tam giác ABC có BC = BA và 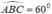 nên tam giác ABC đêù
nên tam giác ABC đêù
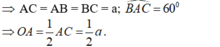
- Trong tam giác OIA có:
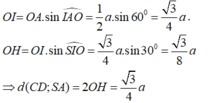

Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ

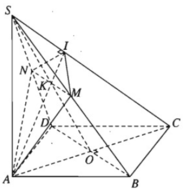
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 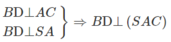
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

a: (SBD) giao (ABCD)=BD
AB vuông góc BD
SB vuông góc BD
=>góc cần tìm là góc SBA

a.
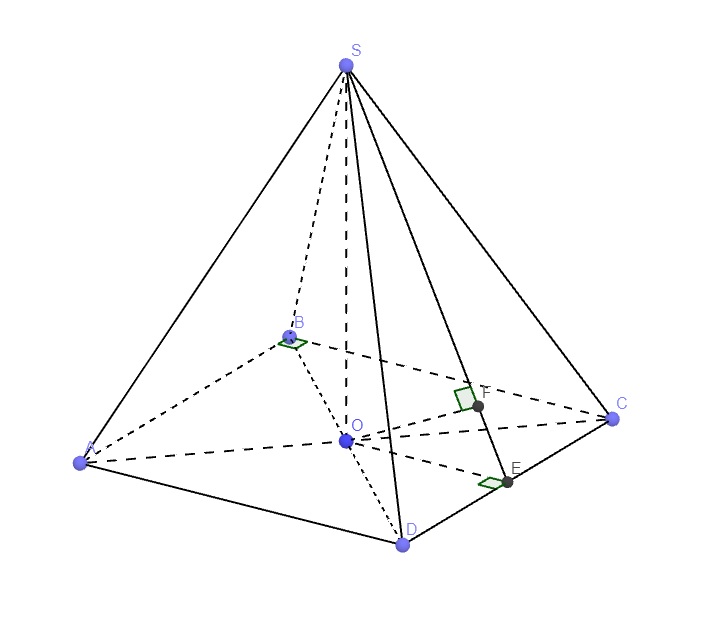
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
Mà \(AC\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b.
\(SO\perp\left(ABCD\right)\Rightarrow OC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCO}\) là góc giữa SC và (ABCD)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\)
\(tan\widehat{SCO}=\dfrac{SO}{OC}=\sqrt{3}\Rightarrow\widehat{SCO}=60^0\)
c.
Gọi E là trung điểm CD, từ O kẻ \(OF\perp SE\)
OE là đường trung bình tam giác BCD \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}BC=a\\OE||BC\Rightarrow OE\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SOE\right)\)\(\Rightarrow CD\perp OF\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
Do \(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF\)
Hệ thức lượng: \(OF=\dfrac{OE.SO}{\sqrt{OE^2+SO^2}}=...\)
D:\(-̣\left(-\dfrac{2}{3}\right)^2\)