Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


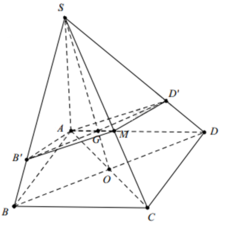
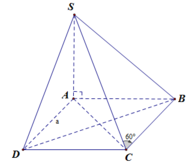
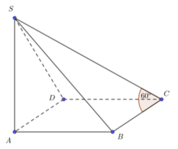
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
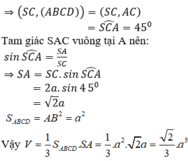

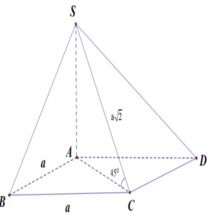
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
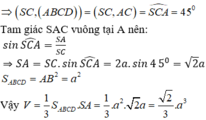

Để tính thể tích SAPMQ, ta cần tìm độ dài đoạn PM và đoạn MQ. Gọi E là trung điểm của BD. Ta có ME song song với AM và ME = 1/2 BD = 1/2 a. Vì (∆) song song với BD nên góc AME = góc ABD = 45 độ. Vì SA vuông góc với ABCD nên góc SAM = 90 độ. Vì SA = a√3 và góc SAM = 90 độ nên tam giác SAM là tam giác vuông cân tại A. Do đó, góc ASM = 45 độ. Vì góc ASM = góc AME = 45 độ nên tam giác ASM và tam giác AME đồng dạng. Vậy, ta có: AM/AS = AE/AM AM^2 = AS * AE AM^2 = (a√3) * (1/2 a) AM^2 = a^2 * √3 / 2 AM = a√3 / √2 AM = a√6 / 2 Ta có ME = 1/2 a Vậy, PM = AM - ME = (a√6 / 2) - (1/2 a) = (a√6 - a) / 2 Tương tự, ta có MQ = AM + ME = (a√6 / 2) + (1/2 a) = (a√6 + a) / 2 Vậy, thể tích SAPMQ = SABC * PM = a^2 * (a√6 - a) / 2 = a^3√6 / 2 - a^3 / 2

Đáp án D
Từ O kẻ OH vuông góc với SC, ta có S C ⊥ ( B D H )
Ta có V S . A H D V S . A C D = S H S C , V S . A H B V S . A C B = S H S C
mà V S . A C D = V S . A C B = 1 2 V S . A B C D = V 2
nên V S . A H D + V S . A H B V 2 = 2 S H S C
⇔ V S . A B H D V = S H S C
Có
B
C
⊥
(
S
A
M
)
nên
![]()
⇒ S A = 3 a 2
Mặt khác: ∆ C A S ~ ∆ C H O
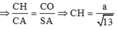
Suy ra S H S C = S C - H C S C = 1 - H C S C = 11 13
⇒ V S . A B H D = 11 13 V
Do đó
V H . B C D = V - V S . A B H D = V = 11 12 V = 2 13 V
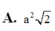
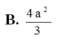
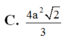
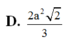

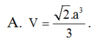
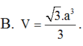
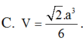
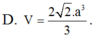

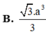
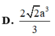



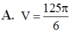
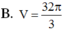
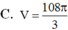
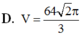

Với thông tin đã cho, ta có Sđ = a^2 và h = SA = 2a. Thay vào công thức, ta có:
Sph = (1/3) * a^2 * 2a = (2/3) * a^3.
Vậy diện tích của hình chóp cắt bởi mặt phẳng (P) là (2/3) * a^3.