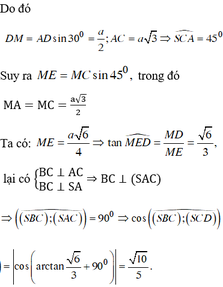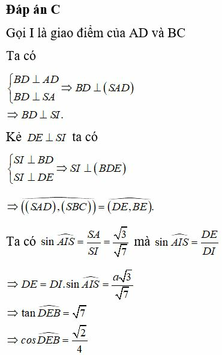Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
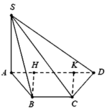
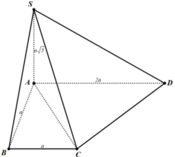
Gọi H, K lần lượt là hình chiếu của B, C trên AD
Gọi α là góc giữa 2 mặt phẳng S A D , S B C
⇒ Δ S H K là hình chiếu của Δ S B C trên S A D ⇒ c o s α = S S H K S S B C
Ta có H K = B C = 2 a ⇒ S S H K = 1 2 S A . H K = a 3 .2 a 2 = a 2 3
Lại có d A ; B C = B H = a 3 ⇒ d S ; B C = a 3 . 2 = a 6
Suy ra S S B C = 1 2 d S ; B C . B C = a 3 6 .
Vậy c o s α = a 3 3 a 3 6 = 2 2

Bài 1 :Diện tích hình tròn bằng bình phương bán kính nhân với Pi. Như vậy, nếu đường kình giảm 50% thì bán kính giảm 50%. Khi đó diện tích sẽ bằng: 50% bán kính( nhân) 50% bán kính (nhân) Pi= 25% bán kính nhân Pi= 25% diện tích hình tròn ban đầu. Như vậy diện tích hình tròn giảm đi: 100%-25%= 75%
Bài 2 : Diện tích hình tròn = Số Pi x R^2
1. Lúc chưa tăng bán kính lên 10% thì:
S(1) = Pi x R^2
2. Khi tăng bán kính lên 10% thì:
S(2) = Pi x (110%. R)^2
S(2) = Pi x (1,1.R)^2
S(2) = Pi x 1,21.R^2
3. Diện tích hình tròn tăng lên là:
S(2) - S(1)
= (Pi x 1,21.R^2) - (Pi x R^2)
= (1,21 x Pi x R^2) - (1 x Pi x R^2)
= (Pi x R^2) x (1,21 - 1)
= 0,21 x Pi x R^2
Mà:
S(1) = Pi x R^2
Nên diện tích tăng lên là: 0,21 x S(1)
Hay nói cách khác là tăng lên 21%
Đáp số: 21%

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

Ta có
xoy + yoz =180o (kề bù)
<=> 5yoz+ yoz=1800
6yoz=180o
=> yoz=30o
=> xoy=5x30=150o
hình bạn tự vẽ nhé
b) Vì ot nằm giữ góc xoy(xoy>xot, 150o>100o) nên:
xot+toy=xoy
100o+yot=150o
yot=50o
Vì ot nằm giữa zox ( zox>tox, 180o>100o) nên
zot+tox=zox
zot+100o=180o
zot=80o

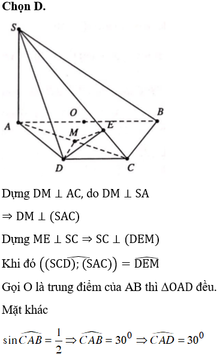
Đáp án C.
Không mất tính tổng quát, giả sử a = 1
Xét hệ trục tọa độ Oxyz với
A 0 ; 0 ; 0 ; D 2 ; 0 ; 0 ;
B 0 ; 1 ; 0 ; S 0 ; 0 ; 5 .
Điểm C thỏa mãn
B C → = 1 2 A D → = 1 ; 0 ; 0
⇒ C 1 ; 1 ; 0 .
mp(SBC) có
n 1 → = S B → ; B C → = 0 ; 1 ; − 5 ; 1 ; 0 ; 0
= 0 ; − 5 ; − 1 .
mp(SCD) có
n 2 → = S D → ; C D → = 2 ; 0 ; − 5 ; 1 ; − 1 ; 0 = 5 ; 5 ; 2 .
Do đó côsin của góc tạo bởi hai mặt phẳng (SBC) và (SCD) bằng:
cos α = n 1 → . n 2 → n 1 . n 2 = 7 2 3 = 21 6 .