Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

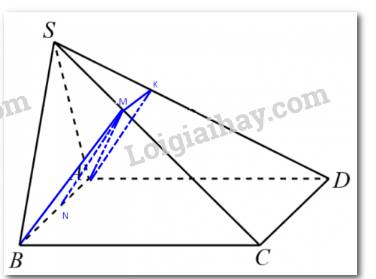
a) Ta có: \(\left( {ABM} \right) \cap \;\left( {ABCD} \right) = AB,\;\left( {ABCD} \right) \cap \;\left( {SCD} \right) = CD,\;AB//CD\).
Suy ra giao tuyến của (ABM) và (SCD) là đường thẳng qua M song song với AB và CD.
Qua M kẻ MK song song với CD (K thuộc SD).
Vậy, K là giao điểm của (AMN) và SD.
Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{SK}}{{SD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
b) Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{MK}}{{CD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
Lại có \(\frac{{AN}}{{AB}} = \frac{1}{3}\), AB=CD suy ra AN = MK.
Xét tứ giác ANMK ta có: AN = MK, AN // MK suy ra ANMK là hình bình hành.
Do đó MN // AK hay MN // (SAD).

Gọi O là tâm đáy \(\Rightarrow\) O là trung điểm BD và AC
Trong mp ((SAC), nối SO cắt AM tại I
\(\Rightarrow I=AM\cap\left(SBD\right)\)
Ta có M là trung điểm SC, O là trung điểm AC
\(\Rightarrow\) I là trọng tâm tam giác SAC
\(\Rightarrow\dfrac{IA}{AM}=\dfrac{2}{3}\Rightarrow\dfrac{MA}{IA}=\dfrac{3}{2}\)

Bài này cũng có thể ứng dụng bài này (vẫn là sử dụng diện tích tam giác):
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
Nhưng đặc biệt hơn 1 chút là nó đi qua điểm A luôn (vậy ta có thể coi như (P) cắt SA tại A và áp dụng nó vẫn đúng):
\(\dfrac{SA}{SA}+\dfrac{SC}{SP}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}=\dfrac{2SO}{SI}=8\)
\(\Rightarrow1+\dfrac{SB}{SN}+\dfrac{SC}{SP}+\dfrac{SD}{SQ}=16\)
\(\Rightarrow\dfrac{SB}{SN}+\dfrac{SC}{SP}+\dfrac{SD}{SQ}=15\)

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

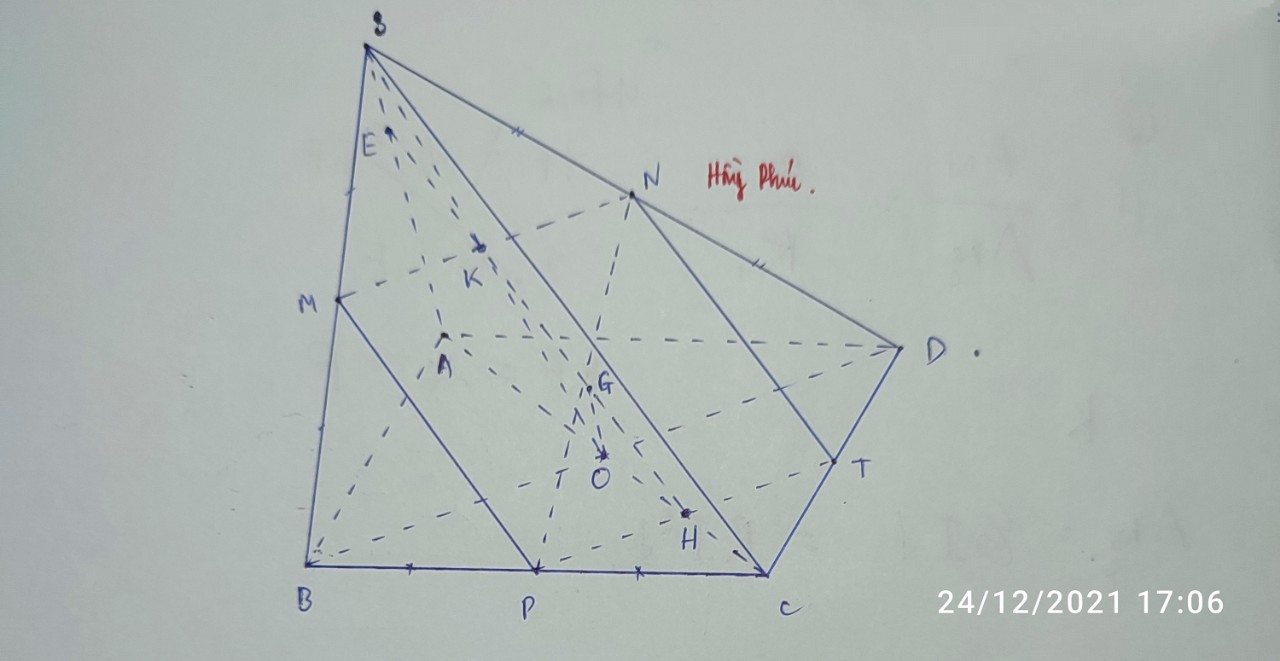
Nối AN kéo dài cắt CD tại E, nối EM kéo dài cắt SD tại I
Do N là trung điểm OB \(\Rightarrow\dfrac{BN}{ND}=\dfrac{1}{3}\)
Áp dụng định lý talet: \(\dfrac{BF}{AD}=\dfrac{BN}{ND}=\dfrac{1}{3}\) \(\Rightarrow\dfrac{CF}{AD}=\dfrac{2}{3}\)
Cũng theo Talet:
\(\dfrac{FC}{FD}=\dfrac{CF}{AD}=\dfrac{2}{3}\) \(\Rightarrow\dfrac{DF}{FC}=\dfrac{3}{2}\)
Áp dụng định lý Menelaus cho tam giác SCD:
\(\dfrac{IS}{ID}.\dfrac{DF}{FC}.\dfrac{CM}{MS}=1\Rightarrow\dfrac{IS}{ID}.\dfrac{3}{2}.1=1\Rightarrow\dfrac{IS}{ID}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{5}\)

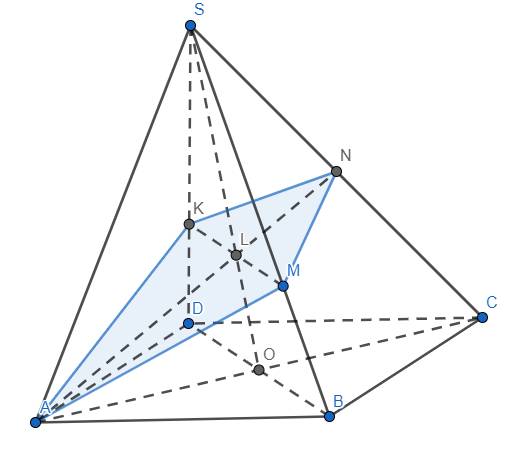
a) Gọi \(O=AC\cap BD\). Khi đó \(O\in\left(SAC\right)\cap\left(SBD\right)\). Lại có \(S\in\left(SAC\right)\cap\left(SBD\right)\) nên SO chính là giao tuyến của (SAC) và (SBD).
b) Trong mp (AMNK) cho \(AN\cap MK=L\). Do \(AN\subset\left(SAC\right),MK\subset\left(SBD\right)\) nên \(L\in\left(SAC\right)\cap\left(SBD\right)\) nên \(L\in SO\). \(\Rightarrow\) L là trọng tâm tam giác SAC \(\Rightarrow\dfrac{SL}{LO}=2\). Mà \(\dfrac{SM}{MB}=2\) nên \(\dfrac{SL}{LO}=\dfrac{SM}{MB}\Rightarrow\) LM//BO hay MK//BD, suy ra đpcm.
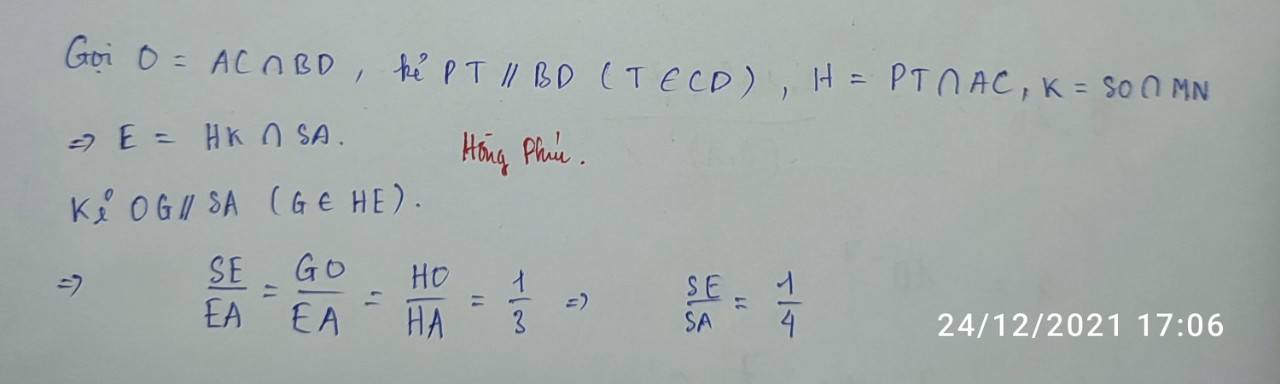
Chọn B