Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B
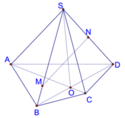
+ Giả sử SO, AD cắt nhau. Khi đó SO, AD đồng phẳng, suy ra S thuộc mp (ABCD) (Vô lý). Đáp án A bị loại.
+ Giả sử MN cắt SC. Khi đó MN và SC đồng phẳng, suy ra C thuộc (SBD) (Vô lý). Do đó đáp án C bị loại.
+ Giả sử SA cắt BC. Khi đó SA, BC đồng phẳng. Suy ra S thuộc mp (ABCD) (Vô lý). Đáp án D bị loại. MN, SO cùng nằm trong mp (SBD), không song song và trùng nhau.
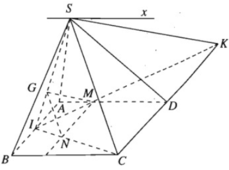
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
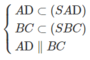
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
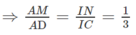
Mà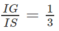 
(G là trọng tâm của ∆SAB) nên
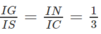⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
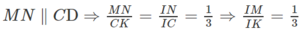
Ta có:
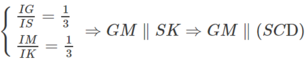
Ta có: Sx là giao tuyến (SAD) và (SBC) sao cho Sx // AD // BC (1)
Có : M, N là trung điểm của AB, CD
Suy ra: MN // AD // BC (2)
Từ (1)(2) suy ra: MN // Sx.
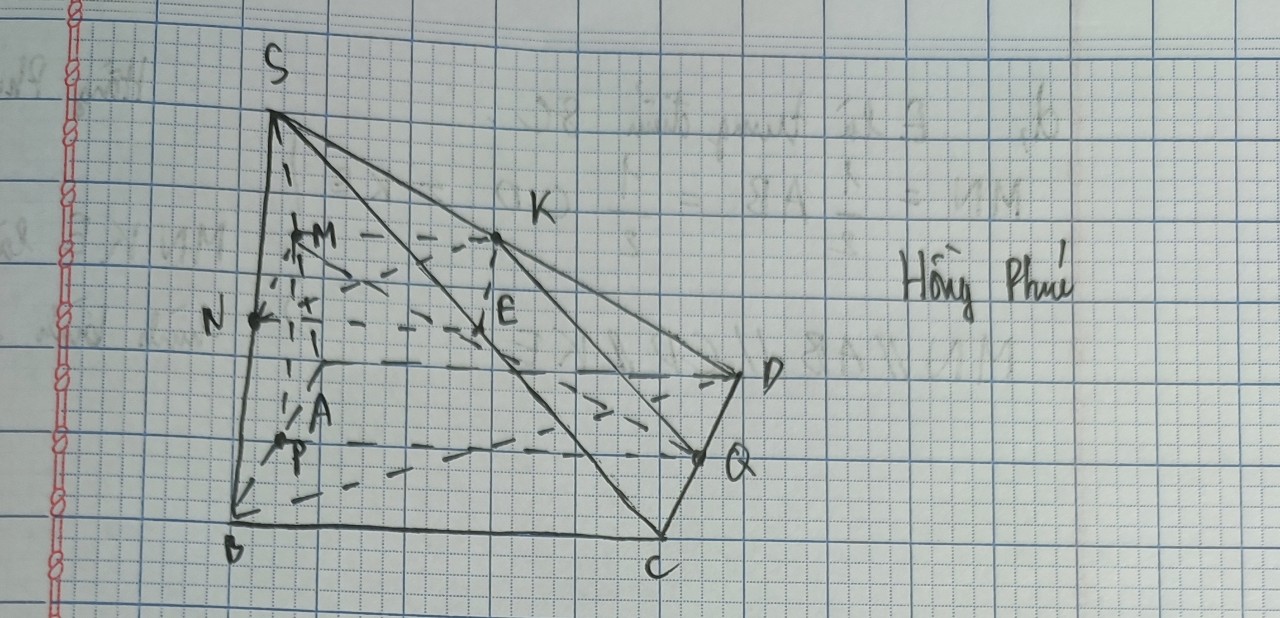
Gọi (P) là mặt phẳng qua M, song song DE và SC
Gọi O là giao điểm AC, BD \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow\) OM là đường trung bình tam giác SAC
\(\Rightarrow OM||SC\Rightarrow O\in\left(P\right)\)
Trong mp (SBD), gọi F là trung điểm BE \(\Rightarrow OF\) là đường trung bình tam giác BDE
\(\Rightarrow OF||DE\Rightarrow F\in\left(P\right)\)
Trong mp (SBC), qua F kẻ đường thẳng song song SC cắt BC tại G
\(\Rightarrow G\in\left(P\right)\)
Trong mp (ABCD), nối GO kéo dài cắt AD tại H
\(\Rightarrow H\in\left(P\right)\)
\(\Rightarrow\) Thiết diện của (P) và chóp là tứ giác MFGH (và tứ giác này không có điều gì đặc biệt)
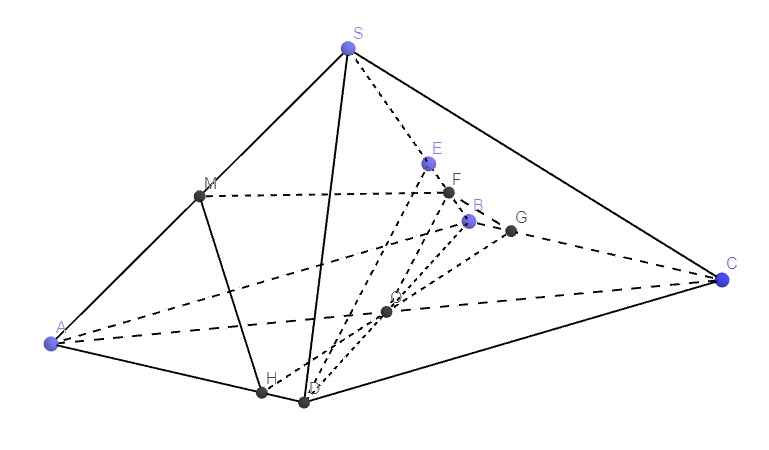
Gọi O là giao điểm AC và BD \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow\) G là trọng tâm tam giác ABC
\(\Rightarrow BG=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BG}{BD}=\dfrac{1}{3}\)
Lại có: \(SM=2MB\Rightarrow2MB=SB-MB\Rightarrow MB=\dfrac{1}{3}SB\Rightarrow\dfrac{MB}{SB}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{BG}{BD}=\dfrac{BM}{SB}=\dfrac{1}{3}\Rightarrow MG||SD\) (Talet đảo)
Mà \(SD\in\left(SAD\right)\Rightarrow MG||\left(SAD\right)\)