Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
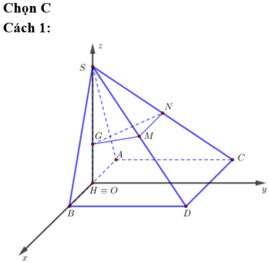
Chọn đáp án C
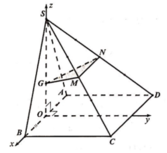
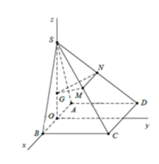
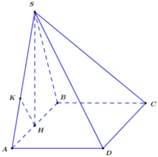
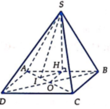
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên
Chọn hệ trục tọa độ Oxyz như hình vẽ. Chọn a = 2.
Khi đó: 
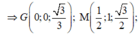
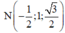
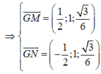
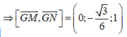
Ta có mặt phẳng (ABCD) có vecto pháp tuyến là 
Mặt phẳng (GMN) có vecto pháp tuyến là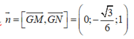 
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD)
Ta có:
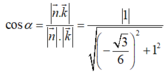
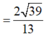
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó
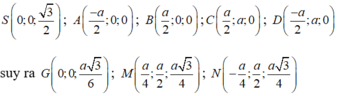
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là 
, mặt phẳng (GMN) có vectơ pháp tuyến là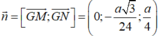 
Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
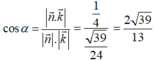
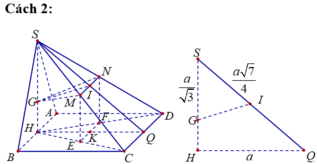
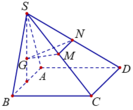
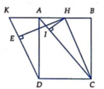
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.
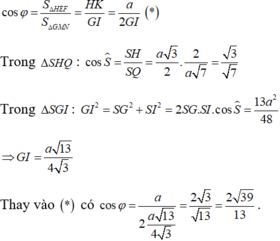
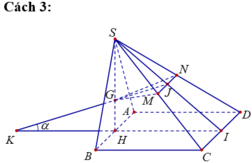
Gọi H, I lần lượt là trung điểm của AB, CD.
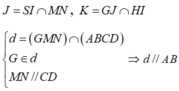
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là 
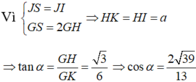
Lớp 12 thì chúng ta tọa độ hóa cho đơn giản
Gọi O là trung điểm AB \(\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(AO=BO=\dfrac{a}{2}\)
Đặt hệ trục Oxyz vào chóp, với gốc O trùng O, tia Oz trùng tia OS, tia Ox trùng tia OB, tia Oy trùng tia ON (với N là trung điểm CD). Quy ước \(\dfrac{a}{2}\) là 1 đơn vị độ dài
Ta được tọa độ các điểm: \(S\left(0;0;\sqrt{3}\right)\) ; \(C\left(1;2;0\right)\) ; \(A\left(-1;0;0\right)\) ; \(D\left(-1;2;0\right)\)
Do M là trung điểm SD \(\Rightarrow M\left(-\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\)
\(\overrightarrow{AM}=\left(\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\) ; \(\overrightarrow{SC}=\left(1;2;-\sqrt{3}\right)\) ; \(\overrightarrow{AC}=\left(2;2;0\right)\)
\(d\left(AM;SC\right)=\dfrac{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right].\overrightarrow{AC}\right|}{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right]\right|}=\dfrac{2\sqrt{5}}{5}=\dfrac{a\sqrt{5}}{5}\)
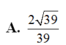
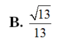
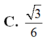
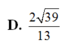
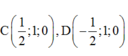
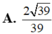
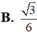
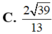
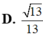
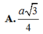
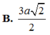
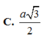
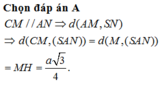
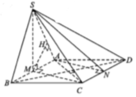
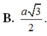
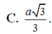
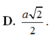
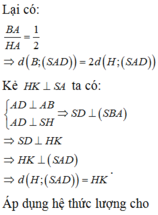
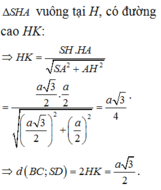
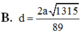
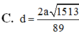
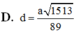
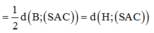
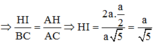
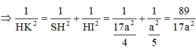
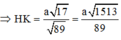
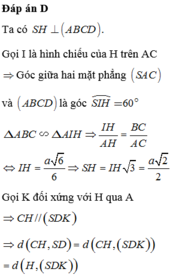
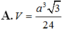
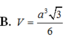
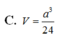
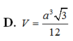
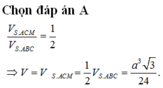
Chọn B.
Gọi Q là trung điểm CD, ta có PQ//SC//MN nên MN//(APQ)
=> d(MN, PQ)=d(MN, (APQ))=d(N,(APQ))
Vì N D ⊥ H C N D ⊥ S H ⇒ N D ⊥ ( S H C )
⇒ N D ⊥ S C ⇒ N D ⊥ P Q
A Q → . N D → = ( A D → + D Q → ) . ( D C → + C N → ) = 0 → ⇒ A Q ⊥ N D
Vậy có
N D ⊥ P Q N D ⊥ A Q ⇒ N D ⊥ A P Q t ạ i E ⇒ d ( M N , A P ) = N E
Mà có
1 D E 2 = 1 D A 2 + 1 D Q 2 = 5 a 2 ⇒ D E = a 5
Và D N = a 5 2 ⇒ E N = 3 a 5 10
Vậy d ( M N , A P ) = 2 a 10