Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

Kẻ M N ∥ B C N ∈ C D , N P ∥ S C P D , M Q ∥ S B Q ∈ S A
⇒ m p a cắt khối chóp S.ABCD theo thiết diện là MNPQ
Ta có M A A B = A Q S A = N D C D = x ⇒ S Q S A = S P S D = 1 − x (Định lý Thalet)
Mà Δ A M N = Δ A D N ⇒ V Q . A M N = V P . A D N = x V S . A M N = x 2 V S . A M N D = x 2 2 V
Và S N . A P Q = 1 3 d N ; S A D . S Δ A P Q = x 1 − x × V N . S A D = x 2 1 − x 2 V
Do đó V A Q M . D P N = V Q . A M N + V P . A N D + V N . A P Q = 3 x 2 − x 3 2 × V = 4 27 V
. ⇒ x 3 − 3 x 2 + 8 27 = 0 ⇒ x = 1 3 Vậy P = 1 − x 1 + x x = 1 3 = 1 2

Đáp án D
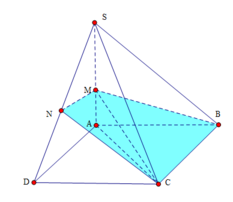
Ta có (BCM) cắt (SAD) theo giao tuyến M N / / A D
V S N M B C V S A B C D = V S M B C + V S M N C V S A B C D
= 1 2 V S M B C V S A B C + V S N M C V S A C D
= 1 2 S M S A + S M S A S N S D = 1 2
⇒ S M S A 2 + S M S A − 1 = 0
⇒ S M S A = 5 − 1 2 ⇔ a − x a = 5 − 1 2
⇒ x = 3 − 5 a

Đáp án B

A C = 2 S A = 2 tan 60 0 = 2 3 V = 1 3 .2 3 .1. 3 = 2


Ta có S C D ∩ A B C D = C D
C D ⊥ S A C D ⊥ A C ⇒ C D ⊥ S A C ⇒ S C ⊥ C D
Vì S C ⊥ C D , S C ⊂ S C D A C ⊥ C D , A C ⊂ A B C D
Nên S C D , A B C D ^ = S C A ^ = 45 o
Dễ thấy ∆ S A C vuông cân tại A
Suy ra SA = AC = a 2
Lại có
S M C D = 1 2 M C . M D = 1 2 a . a = a 2 2
Do đó
V = V S . M C D = 1 3 S M C D S A = 1 3 . a 2 2 . a 2 = a 3 2 6
Ta có
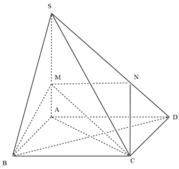
B D ∥ M N M N ⊂ S M N ⇒ B D ∥ S M N
Khi đó d( SM,BD ) = d( SM, (SMN) ) = d( D, (SMN) ) = d( A, ( SMN) )
Kẻ A P ⊥ M N , P ∈ M N A H ⊥ S P , H ∈ S P
Suy ra A H ⊥ S M N ⇒ d A S M N = A H
∆ S A P vuông tại A có
1 A H 2 = 1 S A 2 + 1 A P 2 = 1 S A 2 + 1 A N 2 + 1 A M 2 = 1 2 a 2 + 1 a 2 4 + 1 a 2 = 11 2 a 2
Do đó d = d( SM, BD ) = AH = a 22 11
Đáp án A


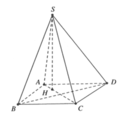
Vẽ S H ⊥ A C tại H.
Khi đó: ( S A C ) ⊥ ( A B C D ) ( S A C ) ⊥ ( A B C D ) = A C S H ⊂ ( S A C ) S H ⊥ A C
⇒ S H ⊥ ( A B C D ) ⇒ V = 1 3 S H . S A B C D
Theo đề ∆ S A C vuông tại S nên ta có:
S C = A C 2 - S A 2 = 6 a 2
và S H = S A . S C A C
= 2 a 2 . 6 a 2 2 a = 6 a 4
Vậy V = 1 3 S H . S A B C D = 6 a 3 12
Chọn đáp án A.







Chọn đáp án C
Lại có MDCN là hình thang vuông tại M và D.
Bằng định lí Talet và Pitago ta tính được