Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải: Gọi H là trung điểm của AC
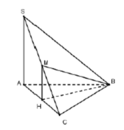
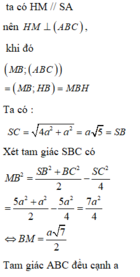
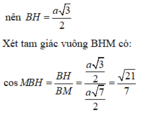

Đáp án C
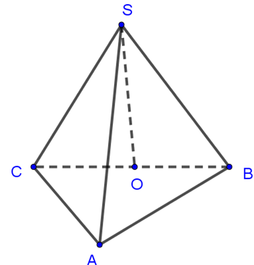
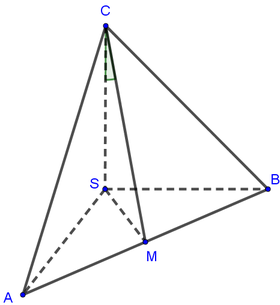
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.
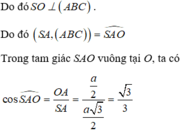

Đáp án C
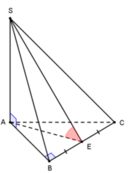
Lấy điểm D sao cho ABCD là hình chữ nhật

Tam giác SAD vuông cân tại A, E là trung điểm SD nên
![]()

Phương pháp:
+) Gọi M, N, P, Q lần lượt là trung điểm của AB, SC, BC, AC. Chứng minh ∠ S A ; B C = ∠ N Q ; M Q
+) Áp dụng định lí cosin trong tam giác MNQ.
Cách giải:
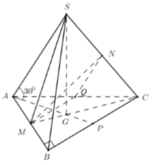


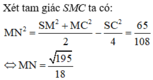
Áp dụng định lý cosin trong tam giác MNQ:
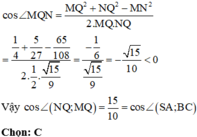
Chú ý: Góc giữa hai đường thẳng là góc nhọn nên cosin của góc giữa hai đường thẳng là giá trị dương.
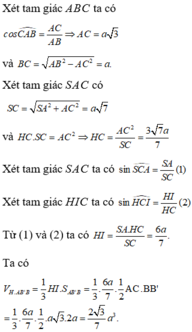


Đáp án B
Phương pháp:
- Cách xác định góc giữa hai mặt phẳng:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
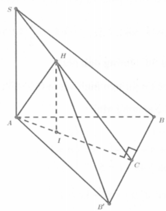
Cách giải: Tam giác ABC vuông tại C có AB = 2a; C A B ^ = 30 0
Tam giác SAC vuông tại A
Vì SA ⊥ (ABC) => (SC;(ABC)) = (SC;AC) = S C A ^