Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

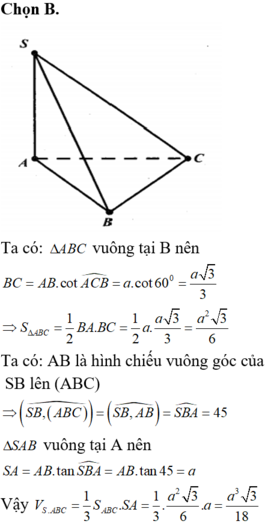
Chọn B.
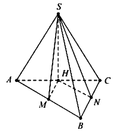
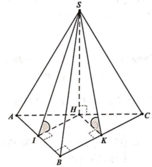
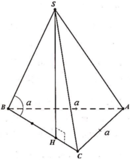
Gọi H là chân đường cao của khối chóp S.ABC.
Lần lượt gọi hình chiếu của H trên các cạnh AB, BC, CA là D, E. F.
Khi đó ta có, góc giữa các mặt phẳng (SAB), (SBC), (SCA) với mặt đáy (ABC) lần lượt là SDH, SHE, SFH và Từ đó suy ra DH = HE = HF. Suy ra H là tâm đường tròn nội tiếp tam giác ABC.
Ta có
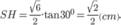 Suy ra
Suy ra 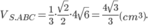
Suy ra chọn B

Đáp án D
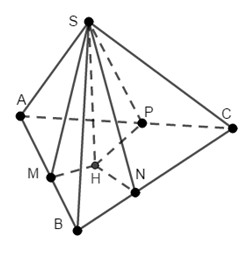
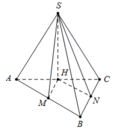
Gọi H là hình chiếu của S trên A C ⇒ S H ⊥ A B C
Kẻ H M ⊥ A B M ∈ A B , H N ⊥ A C N ∈ A C
Suy ra S A B ; A B C ^ = S B C ; A B C ^ = S M H ^ = S N H ^ = 60 °
⇒ ∆ S H M = ∆ S H N ⇒ H M = H N ⇒ H là trung điểm của AC
Tam giác SHM vuông tại H, có tan S M H ^ = S H H M ⇒ S H = a 3 2
Diện tích tam giác ABC là S ∆ A B C = 1 2 . A B . B C = a 2 2
Vậy thể tích cần tính là V = 1 3 . S H . S A B C = 1 3 . a 3 2 . a 2 2 = a 3 3 12





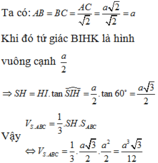

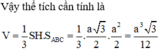

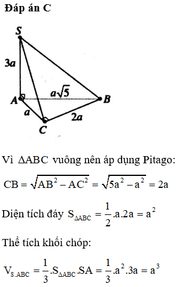
Đáp án D