Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Sử dụng quan hệ vuông góc để chứng minh các đáp án và chọn đáp án đúng.
Cách giải:
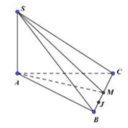
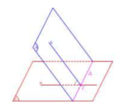
ABC là tam giác cân tại A, M là trung điểm của BC
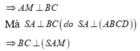
Chọn: C

Đáp án C
Hướng dẫn giải:
Gọi H, K lần lượt là trung điểm của BC và SA.
Dựng đường thẳng d đi qua H và vuông góc với (ABC). Khi đó d//SA.
Trong mặt phẳng (SAH) dựng đường thằng d 1 đi qua K và vuông góc với SA.
Khi đó, d 1 //AH.
Gọi I = d ∩ d 1 tại. Ta có được IA = IB = IC = IS.
Khi đó mặt cầu cần tìm ở đề bài đi qua các điểm A, B, C, S có tâm là I và bán kính là R = IA.
Dễ thấy A H = 1 2 B C = b 2 + c 2 2
và I H = 1 2 S A = a 2 .
Trong ∆ I A H có
![]()
Vậy là ta hoàn thành xong bài toán.

Đáp án C.
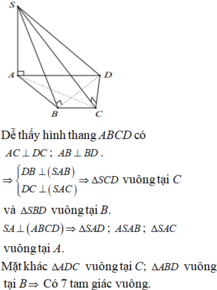
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
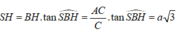
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2

Chọn A
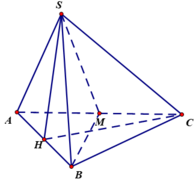
Gọi H là trung điểm của AB. Theo bài ra:
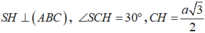
Xét tam giác SCH ta có:


Cho hình chop SABC, có đáy là ABC là tam giác vuông tại B, có độ dài các cạch AB=6,BC=8,SA=10 vuông góc với mặt đáy Tính thể tích khối chóp SABC
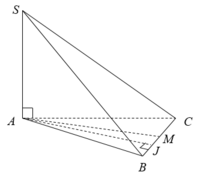
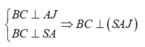
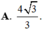
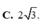
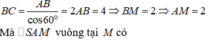
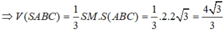
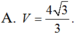

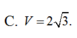
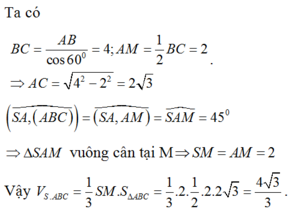
Đáp án A
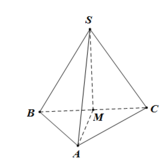
Do S A ⊥ ( A B C ) nên B C ⊥ S A M là trung điểm BC nên ta có B C ⊥ A M
⇒ B C ⊥ ( S A M ) độ dài cạnh hình lập phương là 3cm