Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
![]()
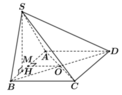
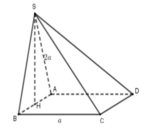
Gọi M là trung điểm AB, do tam giác SAB vuông tại S nên MS = MA = MB
Gọi H là hình chiếu của S trên AB. Từ giả thiết suy ra ![]()
Ta có ![]() nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
Từ (1) và (2) ta có OS = OA = OB = OC = OD.
Vậy O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD bán kính 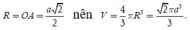
Chọn B.


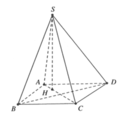
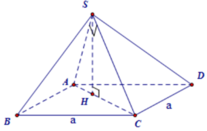
Vẽ S H ⊥ A C tại H.
Khi đó: ( S A C ) ⊥ ( A B C D ) ( S A C ) ⊥ ( A B C D ) = A C S H ⊂ ( S A C ) S H ⊥ A C
⇒ S H ⊥ ( A B C D ) ⇒ V = 1 3 S H . S A B C D
Theo đề ∆ S A C vuông tại S nên ta có:
S C = A C 2 - S A 2 = 6 a 2
và S H = S A . S C A C
= 2 a 2 . 6 a 2 2 a = 6 a 4
Vậy V = 1 3 S H . S A B C D = 6 a 3 12
Chọn đáp án A.

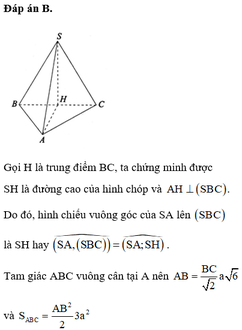
Đáp án B
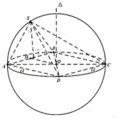
Gọi O là trung điểm của AC, theo bài ra ta có SO là trục của đáy (ABCD).
Trong mặt phẳng (SAC), đường trung trực của SA cắt SO tại I, vậy I là tâm mặt cầu ngoại tiếp chóp SABCD.
Tam giác SMI đồng dạng với tam giác SOA suy ra
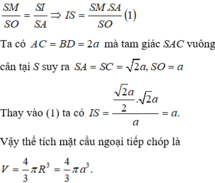
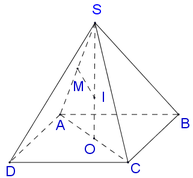

Chọn B.
Phương pháp:
- Xác định đường cao của hình chóp.
- Tính diện tích đáy và chiều cao suy ra thể tích theo công thức V = 1 3 S h



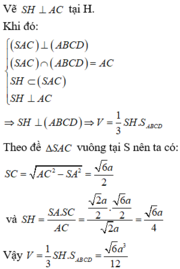
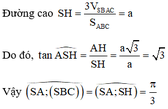


Đáp án C