Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có: f ' x = x − 1 x 2 − 2 2 x 2 + 2 đổi dấu khi đi qua điểm x=1 nên hàm số đã cho có duy nhất 1 điểm cực trị.

Đáp án B
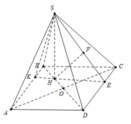
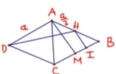
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14

Đáp án A.
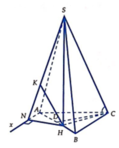
Ta có S C H ^ = 60 ° và
H C = a 7 3 ; S H = H C tan S C H ^ = a 21 3
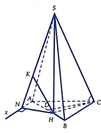
Từ A kẻ tia A x / / C B (như hình vẽ). Khi đó B C / / S A x và do B A = 3 2 H A nên
d B C , S A = d B C , S A x = d B , S A x = 3 2 d H , S A x
Gọi N và K lần lượt là hình chiếu vuông góc của H trên Ax và SN.
Do A N ⊥ S H N và H K ⊥ S N nên H K ⊥ S A N . Khi đó d B C , S A = 3 2 H K .
Ta có
A H = 2 a 3 ; H N = A H sin N A H ^ = a 3 3 .
Suy ra H K = H N . H S H N 2 + H S 2 = a 42 12 . Vậy d B C , S A = a 42 8 .

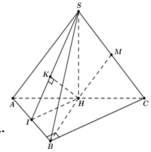
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Đáp án là A.

d B ; S C D = 3 2 d G ; S C D
Tính được: G H = a 3 3 ; S G = a 2 ; G K = a 7 .
Vậy d B ; S C D = 3 2 d G ; S C D = 3 2 . a 7 = 3 a 2 7 .



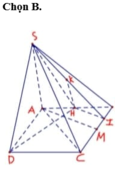
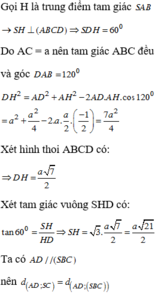



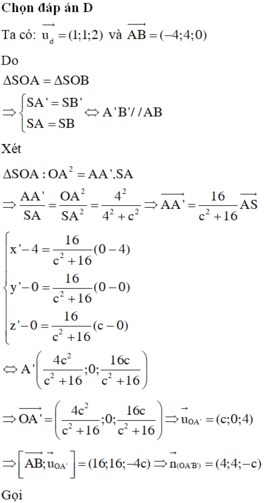
Từ giả thiết suy ra: hình chóp S.ABC là hình chóp đều.
Gọi G là trọng tâm tam giác A B C ⇒ S G ⊥ A B C D
A B / / C D ⇒ A B / / S C D ⇒ d A B ; S C = d A B ; S C D = d B ; S C D = 3 2 d G ; S C D
(Vì B D G D = 3 2 ).
Trong mp (ABCD) vẽ G C ⊥ C D , C D ⊥ S G ⇒ C D ⊥ S G C ⇒ S G C ⊥ S C D
Mà S G C ∩ S C D = S C , vẽ G H ⊥ S C ⇒ d G ; S C D = G H
G B = G C = 2 3 . a 3 2 = a 3 3 .
⇒ S G = S B 2 − B G 2 = 4 a 2 − a 2 3 = a 11 3
Tam giác SHG vuông tại G:
1 G H 2 = 1 S G 2 + 1 G C 2 = 3 11 a 2 + 3 a 2 = 36 11 a 2 ⇒ G H = a 11 6
Vậy d A B ; S C = a 11 4