K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
2 tháng 1 2017
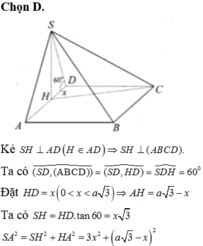
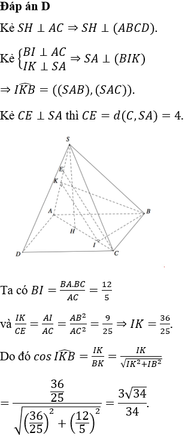
Đáp án D
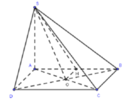
Phương pháp:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
Gọi H là trung điểm của AB => OH//AD
ABCD là hình vuông => AD ⊥ AB; OH ⊥ AB
Mà OH ⊥ SA, (vì SA ⊥ (ABCD))
=> OH ⊥ (SAB)
=>SH là hình chiếu vuông góc của SO trên mặt phẳng (SAB)
=> (SO,(SAB)) = (SO,SH) = HSO
Ta có: OH là đường trung bình của tam giác ABD 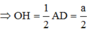
Tam giác SAH vuông tại A ![]()
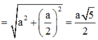
Tam giác SHO vuông tại H: 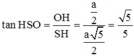


CM
3 tháng 12 2019
Trong tam giác SOC, kẻ OK ⊥ OS(như hình vẽ).(1)
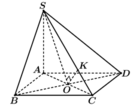
Dễ dàng chứng minh được ![]()
![]()
![]()
Ta tính được 
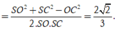
Chọn B.

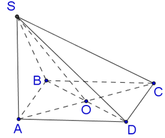

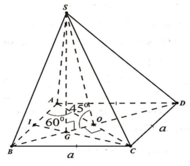
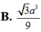





Đáp án D
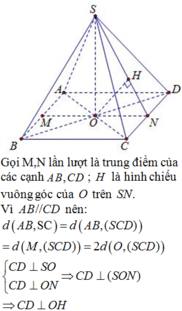
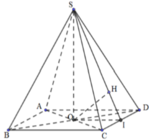
Ta có A C = 2 a = S A = S C suy ra tam giác SAC đều, do đó S O = 2 a 3 2 = a 3 . Vẽ D J ⊥ S C , J ∈ S C . Khi đó BJ vuông góc với SC.
Ta có: S C D ∩ S C A = S C , J D ⊥ S C , J B ⊥ S C . Đặt δ = D J B ^ . Vì JD = JB nên JO là đường cao của tam giác cân DJB, suy ra JO cũng là đường phân giác. Do đó góc giữa (SDC) và (SAC) là D I O ^ = δ 2 .
Ta có S C ⊥ D J B , mà O J ⊂ D J B nên O J ⊥ S C . Trong Δ D J O ta có: O J = O D . cot δ 2 . Trong Δ S O C ta có: 1 O J 2 = 1 O S 2 + 1 O A 2 ⇔ 1 a 2 cot 2 δ 2 = 1 3 a 2 + 1 a 2
Do đó: 1 a 2 cot 2 δ 2 = 4 3 a 2 ⇔ cot 2 δ 2 = 3 4 ⇔ 1 + cot 2 δ 2 = 7 4
⇔ 1 sin 2 δ 2 = 7 4 ⇔ sin 2 δ 2 = 4 7 ⇔ cos 2 δ 2 = 3 7
Mà cos δ 2 > 0 nên từ (1) ta có cos δ 2 = 21 7 . Vậy côsin của góc giữa (SDC) và ( S A C ) bằng 21 7