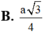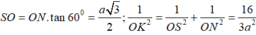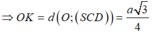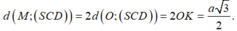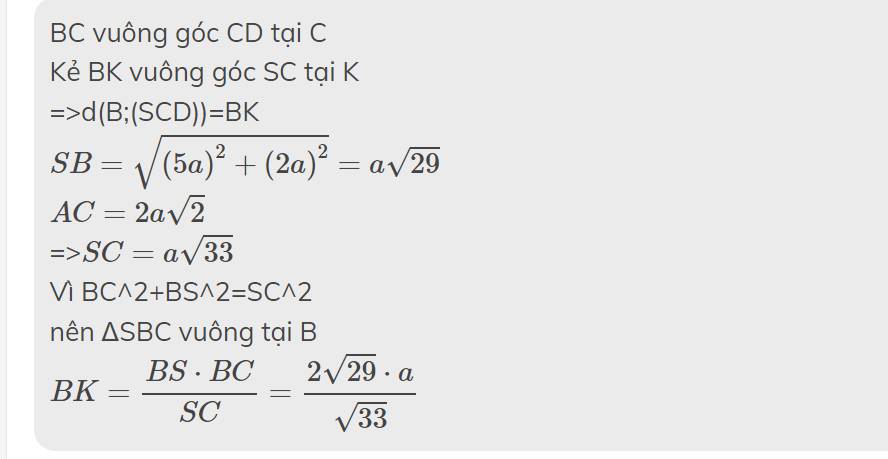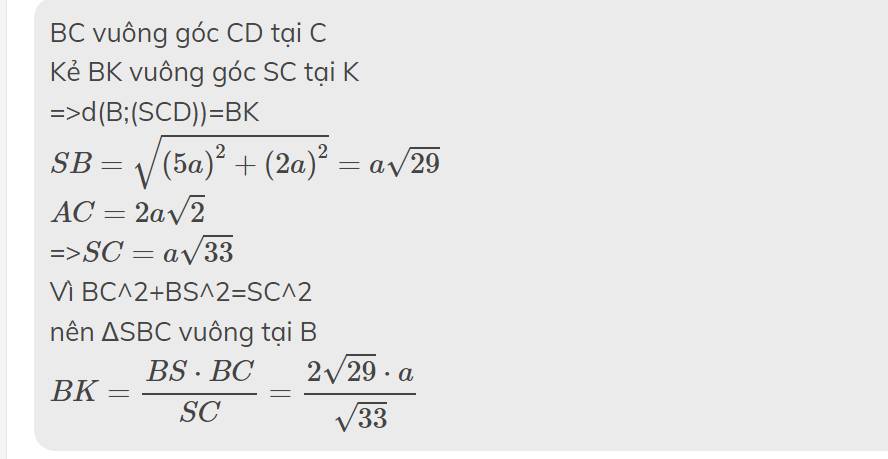Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì SABC là hình chóp đều nên nó sẽ có tính đối xừng, và cách làm giống bài bên trên toi vừa làm, bạn tham khảo

Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp BC\)
Mà \(BC\perp AB\Rightarrow BC\perp\left(SAB\right)\)
Gọi K là trung điểm CD \(\Rightarrow HK||BC\Rightarrow HK\perp AB\Rightarrow HK\perp\left(SAB\right)\)
Trong tam giác SHK, kẻ \(HI\perp SK\Rightarrow HI\perp\left(SCD\right)\)
\(\Rightarrow HI=d\left(H;\left(SCD\right)\right)\)
Mà \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=HI\)
\(SH=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) ; \(HK=BC=a\)
\(\dfrac{1}{HI^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}=\dfrac{7}{3a^2}\Rightarrow HI=\dfrac{a\sqrt{21}}{7}\)
b. Theo cmt ta có \(BC\perp\left(SAB\right)\Rightarrow d\left(C;\left(SAB\right)\right)=BC=a\)
c. \(BC||AD\Rightarrow d\left(C;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà BH cắt (SAD) tại A, đồng thời \(BA=2HA\Rightarrow d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)\)
Từ H kẻ \(HM\perp SA\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM=d\left(H;\left(SAD\right)\right)\)
\(\dfrac{1}{HM^2}=\dfrac{1}{SH^2}+\dfrac{1}{AH^2}=\dfrac{16}{3a^2}\Rightarrow HM=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow d\left(C;\left(SAD\right)\right)=2HM=\dfrac{a\sqrt{3}}{2}\)

Gọi O là tâm đáy, M là trung điểm AB và H là hình chiếu vuông góc của S lên (ABCD)
\(\Rightarrow\) H trùng tâm của tam giác đều ABC đồng thời HM là trung tuyến (kiêm đường cao) của tam giác ABC
\(\widehat{DCH}=\widehat{ACH}+\widehat{ACD}=\dfrac{1}{2}\widehat{ACB}+\widehat{ACD}=\dfrac{1}{2}.60^0+60^0=90^0\)
\(\Rightarrow HC\perp CD\)
\(\Rightarrow CD\perp\left(SCH\right)\Rightarrow\widehat{SCH}\) là góc giữa (SCD) và (ABCD) \(\Rightarrow\widehat{SCH}=60^0\)
\(CH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow SH=CH.tan60^0=a\)
\(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(AB;SD\right)=d\left(AB;\left(SCD\right)\right)=d\left(M;\left(SCD\right)\right)\)
MH cắt (SCD) tại C, mà \(CM=\dfrac{3}{2}CH\Rightarrow d\left(M;\left(SCD\right)\right)=\dfrac{3}{2}d\left(H;\left(SCD\right)\right)\)
Trong tam giác vuông SCH, kẻ \(HK\perp SC\Rightarrow HK\perp\left(SCD\right)\Rightarrow HK=d\left(H;\left(SCD\right)\right)\)
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{CH^2}=\dfrac{4}{3a^2}\Rightarrow HK=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(AB;SD\right)=\dfrac{3a\sqrt{3}}{4}\)

BC vuông góc CD tại C
Kẻ BK vuông góc SC tại K
=>d(B;(SCD))=BK
\(SB=\sqrt{\left(5a\right)^2+\left(2a\right)^2}=a\sqrt{29}\)
\(AC=2a\sqrt{2}\)
=>\(SC=a\sqrt{33}\)
Vì BC^2+BS^2=SC^2
nên ΔSBC vuông tại B
\(BK=\dfrac{BS\cdot BC}{SC}=\dfrac{2\sqrt{29}\cdot a}{\sqrt{33}}\)