Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sxq=1/2*40*13=20*13=260cm2
Độ dài cạnh ở đáy là 40/4=10cm
V=10^2*12=1200cm3

Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)

Gọi \(a\) là cạnh đáy hình chóp tứ giác đều \(\left(cm\right)\)
\(h\) là chiều cao hình chóp tứ giác đều \(\left(cm\right)\)
\(d\) là trung đoạn\(\left(cm\right)\)
Ta có :
\(S_{xq}=4S=4.\dfrac{1}{2}a.d=2ad\)
mà \(d^2=h^2+\dfrac{a^2}{4}\Rightarrow d=\sqrt[]{h^2+\dfrac{a^2}{4}}\)
\(\Rightarrow S_{xq}=2a\sqrt[]{h^2+\dfrac{a^2}{4}}\)
\(\Leftrightarrow S^2_{xq}=4a^2\left(h^2+\dfrac{a^2}{4}\right)=4a^2h^2+a^4\)
\(\Leftrightarrow a^4+4a^2h^2-S^2_{xq}=0\)
\(\Leftrightarrow a^4+4a^2.36-36^2=0\)
\(\Leftrightarrow a^4+144a^2-1296=0\left(1\right)\)
\(\Delta'=5184+1296=6480\Rightarrow\sqrt[]{\Delta'}=36\sqrt[]{5}\)
Pt (1) có nghiệm \(a^2=-72+36\sqrt[]{5}=36\left(1-\sqrt[]{5}\right)\)
\(\)\(\Rightarrow a=6\sqrt[]{1-\sqrt[]{5}}\left(cm\right)\) (cạnh đáy là hình vuông)
Vậy cạnh đáy tứ giác đều là \(a=6\sqrt[]{1-\sqrt[]{5}}\left(cm\right)\)
Đính chính
\(...a^2=-72+36\sqrt[]{2}=36\left(\sqrt[]{5}-2\right)\)
\(\Rightarrow a=6\sqrt[]{\sqrt[]{5}-2}\left(cm\right)\)
Vậy cạnh tứ giác đều là \(a=6\sqrt[]{\sqrt[]{5}-2}\left(cm\right)\)

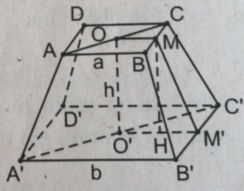
Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
S x q = 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′=
a
2
+
b
2
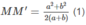
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
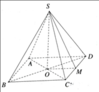
Trong tam giác vuông MHM' ta có: M M ' 2 = M H 2 + H M ' 2 = h + b - a / 2 2 (2)
Từ (1) và (2) suy ra :
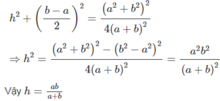

Thể tích là:
\(V=\dfrac{1}{3}\cdot36\cdot9=12\cdot9=108\left(cm^3\right)\)