Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \)
\(\overrightarrow {OD} - \overrightarrow {OC} = \overrightarrow {CD} \)
Do ABCD là hình bình hành nên \(\overrightarrow {BA} = \overrightarrow {CD} \)
Suy ra, \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OD} - \overrightarrow {OC} \)
b) \(\overrightarrow {OA} - \overrightarrow {OB} + \overrightarrow {DC} = (\overrightarrow {OD} - \overrightarrow {OC}) + \overrightarrow {DC} \\= \overrightarrow {CD} + \overrightarrow {DC} = \overrightarrow {CC} = \overrightarrow 0 \)

a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).

a) ABCD là hình bình hành nên \(\overrightarrow {DC} = \overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0 \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {MD} + \overrightarrow {DC} } \right)\)
\(= \left( {\overrightarrow {MB} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BA} + \overrightarrow {DC}} \right)\)
\(= \overrightarrow {MB} + \overrightarrow {MD} \) (Vì \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0} \))

a) Chứng minh \(\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AD}\)
Ta có: \(\overrightarrow{AC}-\overrightarrow{CD}=\overrightarrow{AD}\left(đpcm\right)\) ( vì \(\overrightarrow{BA}=\overrightarrow{CD}\) )
b) Chứng minh \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AC\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) ( theo quy tắc hình bình hành )
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC\left(đpcm\right)\)
bài này chả khó áp dụng 1 bước là ra ngay điều cần chứng minh rồi


a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
\( \Leftrightarrow \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} = 4\overrightarrow {MO} \)
\( \Leftrightarrow 4\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) = 4\overrightarrow {MO} \)
\( \Leftrightarrow 4\overrightarrow {MO} + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MO} \\ \Leftrightarrow 4\overrightarrow {MO} = 4\overrightarrow {MO} \) (luôn đúng)
(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)
b) ABCD là hình bình hành nên ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\)\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC} \) (đpcm)

\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OA}+\overrightarrow{OC}\right)+\left(\overrightarrow{OB}+\overrightarrow{OC}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}\)(Theo tính chất hình bình hành).
\(=\overrightarrow{0}\) .

a: \(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{AD}\)
b: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{BD}-\overrightarrow{BD}=\overrightarrow{0}\)

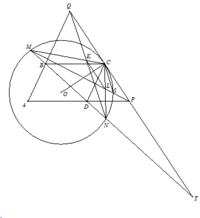
Gọi MP giao (O) tại điểm thứ hai S
Ta có các biến đổi góc sau:
K M L ^ = C M S ^ = S C P ^ (góc tạo bởi tiếp tuyến và dây cung)
= M S C ^ − S P C ^ (góc ngoài)
= M N C ^ − M N Q ^ (do các tứ giác MNPQ và MNSC nội tiếp).
= K N L ^
Từ đó tứ giác MKLN nội tiếp, suy ra K L M ^ = K N M ^ = Q P M ^ ⇒ K L ∥ P Q ⊥ O C
Vậy K L ⊥ O C .