Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

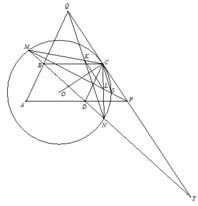
1). Gọi MN giao PQ tại T. Theo định lí Thales, ta có T P T C = T D T B = T C T Q .
Từ đó T C 2 = T P . T Q .
Do TC là tiếp tuyến của (O), nên T C 2 = T M . T N .
Từ đó T M . T N = T C 2 = T P . T Q , suy ra tứ giác MNPQ nội tiếp.

![]() .
.
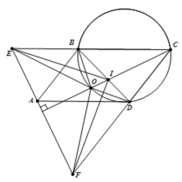
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .

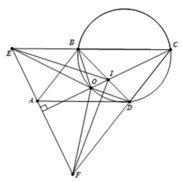
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó
O
E
=
O
C
=
O
F
, vậy O là tâm đường tròn ngoại tiếp tam giác ![]() .
.

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
hay OA\(\perp\)BC
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔDBA vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2=4R^2\)


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

a) BC vuông góc với AO là theo tính chất hai tiếp tuyến đi qua 1 điểm A
b) Xét hai tam giác DCO và DBA có góc D chung và góc C = góc B = 90 độ (tính chất tiếp tuyến)
=> tam giác DCO đồng dạng với tam giác DBA
=> DC/DB = DO/DA
=> DC.DA = DO.DB (đpcm)
c) Vì OM vuông góc với DB => OM // BA (cùng vuông góc với DB)
Ta có AM/DM + 1 = (AM + DM)/DM = DA/DM
Theo Viet ta có: DA/DM = AB/MO
=> AM/DM + 1 = AB/OM
=> AB/OM - AM/DM = 1 (*)
Ta lại có tam giác MOA cân (vì góc MOA = góc BAO do so le trong, góc MAO = góc BAO do tính chất hai tiếp tuyến cùng 1 điểm)
=> OM = AM
(*) trở thành: AB/AM - AM/DM = 1 (đpcm)

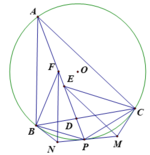
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.
Gọi MP giao (O) tại điểm thứ hai S
Ta có các biến đổi góc sau:
K M L ^ = C M S ^ = S C P ^ (góc tạo bởi tiếp tuyến và dây cung)
= M S C ^ − S P C ^ (góc ngoài)
= M N C ^ − M N Q ^ (do các tứ giác MNPQ và MNSC nội tiếp).
= K N L ^
Từ đó tứ giác MKLN nội tiếp, suy ra K L M ^ = K N M ^ = Q P M ^ ⇒ K L ∥ P Q ⊥ O C
Vậy K L ⊥ O C .