Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xem ở đây nha:
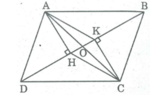
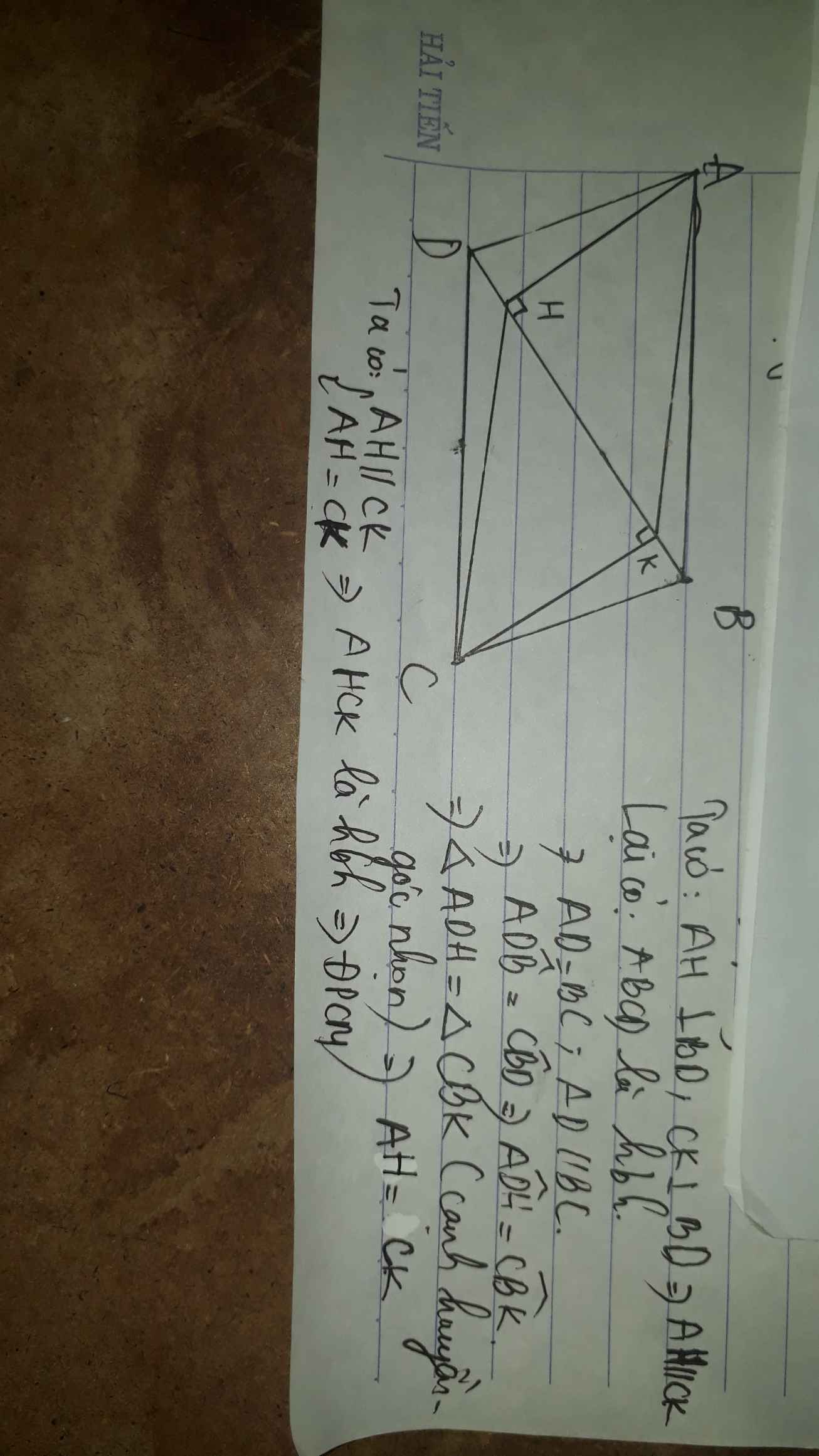
Cho hình bình hành ABCD, Gọi H và K lần lượt là hình chiếu của A và C lên đường chéo BD. a) Chứng minh AHCK là hình bình hành. b) Gọi O là trung điểm của HK. Chứng minh ba điểm A, O, C thẳng hàng - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
Xét tam giác vuông ADH & tam giác vuông CKB:
AD = BC ( ABCD là hbh)
góc D1= góc B1 ( so le trong)
=> tam giác vuông = tam giác vuông CKB ( cạnh hyền - góc nhọn)
=> AH = CK ( 2 cạnh t/ứng)
Xét tứ giác AHCK :
AH = CK (cmt)
AH // CK ( cùng vuông góc vs BD)
=> AHCK là hình bình hành ( đn)

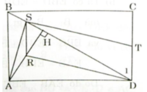
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
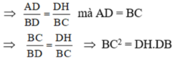
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
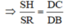
![]()
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o

Ta chứng minh AH//CK, AH = CK (DAHD = DCKB) Þ AHCK là hình bình hành (cặp cạnh đối song song và bằng nhau)


Ta có:
△ ABC = △ ADC (c.c.c) ⇒ S A B C = S A D C (1)
△ AHC = △ AKC (c.c.c) ⇒ S A H C = S A K C (2)
Từ (l) và (2) ⇒ S A B C + S A H C = S A D C + S A K C
Hay S A B C H = S A D C K

a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
mà AH//CK
nên AHCK là hình bình hành
b: AHCK là hbh
=>AC cắt HK tại trung điểm của mỗi đường
=>A,O,C thẳng hàng

a) Chứng minh các cặp tam giác bằng nhau:
DABH = DCDK và DBCH = DDAK
Từ đó, suy ra AABH + SBCH = SCDH + SDAK
Þ ĐPCM.
b) Trừ cả 2 vế của ý a) cho SAKCH, ta thu được SABCK = SADCH