Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình mik ko vẽ đc xl!!!(GT+KL cx vậy)
a)Ta có AD//BN(NϵBC) => \(\frac{AM}{AB}=\frac{DM}{DN}\)(dl ta-lét) \(_1\)
Lại có BM//DC(MϵAB) => \(\frac{CB}{CN}=\frac{DM}{DN}\)(dl ta-lét) \(_2\)
từ 1 và 2 => \(\frac{AM}{AB}=\frac{DM}{DN}=\frac{CB}{CN}\left(đpcm\right)\)
b) ta có: AM//DC(MϵAB) => \(\frac{DI}{IM}=\frac{BC}{AM}=\frac{AB}{AM}\)(hệ quả ; BC=AB)
CMTT => \(\frac{IN}{DI}=\frac{NC}{DA}=\frac{NC}{CB}\)
VÌ \(\frac{NC}{CB}=\frac{AB}{AM}\left(cmt\right)\)
\(\Rightarrow\frac{IN}{ID}=\frac{ID}{IM}\Leftrightarrow ID^2=IN\cdot IM\left(đpcm\right)\)
câu b sai rồi nhé, DC/AM chứ không phải là BC/AM và DC=AB( 2 cạnh đối của HBH)

Tham khảo bài này nha!
Hình thang ABCD (AB//CD) có AC va BD cắt nhau tại O , AD và BC cắt nhau tại K . Chứng minh rằng OK đi qua trun?
Tứ giác ABCD là hình thang nên:AB//CD.
Gọi M, N lần lượt là giao điểm của KO với AB,CD.
Áp dụng định lý talet ta có:
AM/DN=MB/NC(=KM/KN)
=(AM+MB)/(CN+ND) (t/c dãy tỉ số bằng nhau) =AB/DC.
=AO/OC=AM/NC.
Vậy AM/DN=AM/NC hay DN=NC.
tương tự MB=MA.
hay ta có OK đi qua trung điểm của AB và CD.
: Tứ giác ABCD là hình thang nên:AB//CD.
Gọi M, N lần lượt là giao điểm của KO với AB,CD.
Áp dụng định lý talet ta có:
AM/DN=MB/NC(=KM/KN)
=(AM+MB)/(CN+ND) (t/c dãy tỉ số bằng nhau) =AB/DC.
=AO/OC=AM/NC.
Vậy AM/DN=AM/NC hay DN=NC.
tương tự MB=MA.
ta có OK đi qua trung điểm của AB và CD.

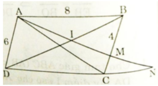
a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
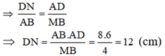
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên
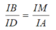
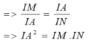

a)
Áp dụng Ta-lét vào tam giác ADM và MNB,vì AD//BN,ta có: \(\frac{AM}{MB}=\frac{DM}{DN}\)(1)
Áp dụng Ta-lét vào tam giác DNC ,vì MB//DC, ta có : \(\frac{DM}{DN}=\frac{CB}{CN}\)(2)
Từ (1),(2), ta có: \(\frac{AM}{MB}=\frac{DM}{DN}=\frac{CB}{CN}\)(đpcm)
b)
Áp dụng Ta-lét vào tam giác AMI và IDC,vì AM//DC ,ta có: \(\frac{DI}{IM}=\frac{IC}{AI}\)(1)
Áp dụng Ta-lét vào tam giác IAD và INC , vì AD//NC , ta có :\(\frac{IN}{ID}=\frac{IC}{AI}\)(2)
Từ (1),(2); ta có : \(\frac{ID}{IM}=\frac{IN}{ID}\)\(\Rightarrow\)IM.IN=ID2.