Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

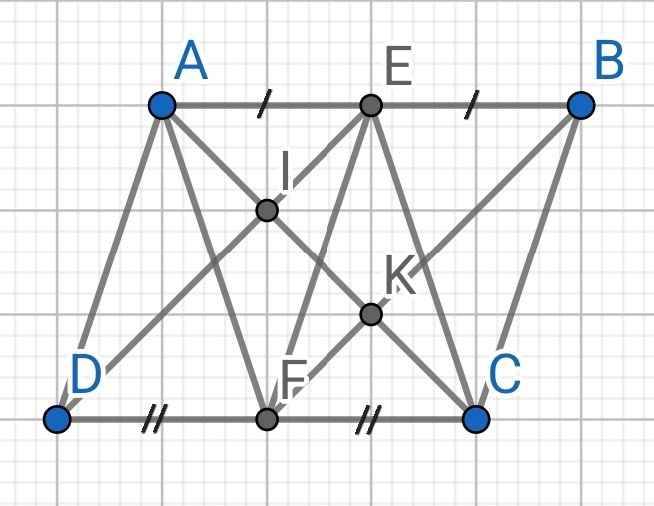 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC

Câu 2:
a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>BDEC là hình thang
mà góc B=góc C
nên BDEC là hình thang cân
b: Xét ΔDEB có
N là trung điểm của DE
M là trung điểm của DB
Do đó: MN là đường trung bình
=>MN//EB và MN=EB/2(1)
Xét ΔECB có
P là trung điểm của EC
Q là trung điểm của BC
Do đó: PQ là đường trung bình
=>PQ//BE và PQ=BE/2(2)
từ (1) và (2) suy ra MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔDEC có
N là trung điểm của DE
P là trung điểm của EC
Do đó: NP là đường trung bình
=>NE=DC/2=NM
=>NMQP là hình thoi
a) Vì ABCD là hình bình hành\(\Rightarrow AB//CD\)
mà \(E\in CD,F\in CD\)\(\Rightarrow AE//DF,BE//CF\left(đpcm\right)\)
b) ABCD là hình bình hành \(\Rightarrow AB=CD\)
mà \(AE=DF\left(gt\right)\)\(\Rightarrow BE=CF\left(đpcm\right)\)
c) Tứ giác AEFD có AE // DF, AE = DF
\(\Rightarrow\)Tứ giác AEFD là hình bình hành (đpcm)
d) Chứng minh tương tự phần c ta suy ra đpcm
TÔi cần hình của bài này