Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔABM=ΔCDM
b: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD

bn tự vẽ hình nhé
a)Xét tam giác ACK và tam giác ABH:
góc K=góc H(=90độ)
AB=AC(gt)
góc A chung
vậy 2 tam giác này bằng nhau (cgv.gnk)

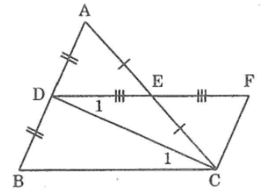
Ta có: ΔADE= ΔCFE(chứng minh trên)
⇒∠(ADE) =∠(CFE) (hai góc tương ứng)
Suy ra: AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ΔBDC và ΔFCD, ta có:
BD = CF (chứng minh trên)
∠(BDC) =∠(FCD) (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ΔBDC= ΔFCD (c.g.c)

a) Xét Δ AIB và Δ CID:
+ IB = ID (gt).
+ IA = IC (I là trung điểm của AC).
+ ^AIB = ^CID (2 góc đối đỉnh).
=> Δ AIB = Δ CID (c - g - c).
b) Xét tứ giác ABCD có:
+ I là trung điểm của AC (gt).
+ I là trung điểm của BC (IB = ID).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AD = BC và AD // BC (Tính chất hình bình hành).
c) Xét tứ giác KABC có:
+ E là trung điểm của AB (gt).
+ E là trung điểm của KC (EC = EK).
=> Tứ giác KABC là hình bình hành (dhnb).
=> KA // BC (Tính chất hình bình hành).
Mà AD // BC (cmt).
=> 3 điểm D, A, K thẳng hàng (đpcm).

a) Xét ΔNAC và ΔNDB, có:a) Xét ΔNAC và ΔNDB, có:
AN = DN (gt)AN = DN (gt)
ˆANC = ˆBND (2 góc đối đỉnh)ANC^ = BND^ (2 góc đối đỉnh)
NC = BN (N là trung điểm của BC)NC = BN (N là trung điểm của BC)
⇒ ΔNAC = ΔNDB (c.g.c)
a: Xét ΔNAC và ΔNDB có
NA=ND
\(\widehat{ANC}=\widehat{DNB}\)
NC=NB
Do đó: ΔNAC=ΔNDB
b: Xét tứ giác ABDC có
N là trung điểm của BC
N là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
mà N là giao điểm của AD và BC
nên ND=NC


Xét ΔAID và ΔCKB có
AD=CB
góc D=góc B
DI=KB
=>ΔAID=ΔCKB
Xét ΔAIK và ΔCKI có
AI=CK
AK=CI
IK chung
=>ΔAIK=ΔCKI