Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
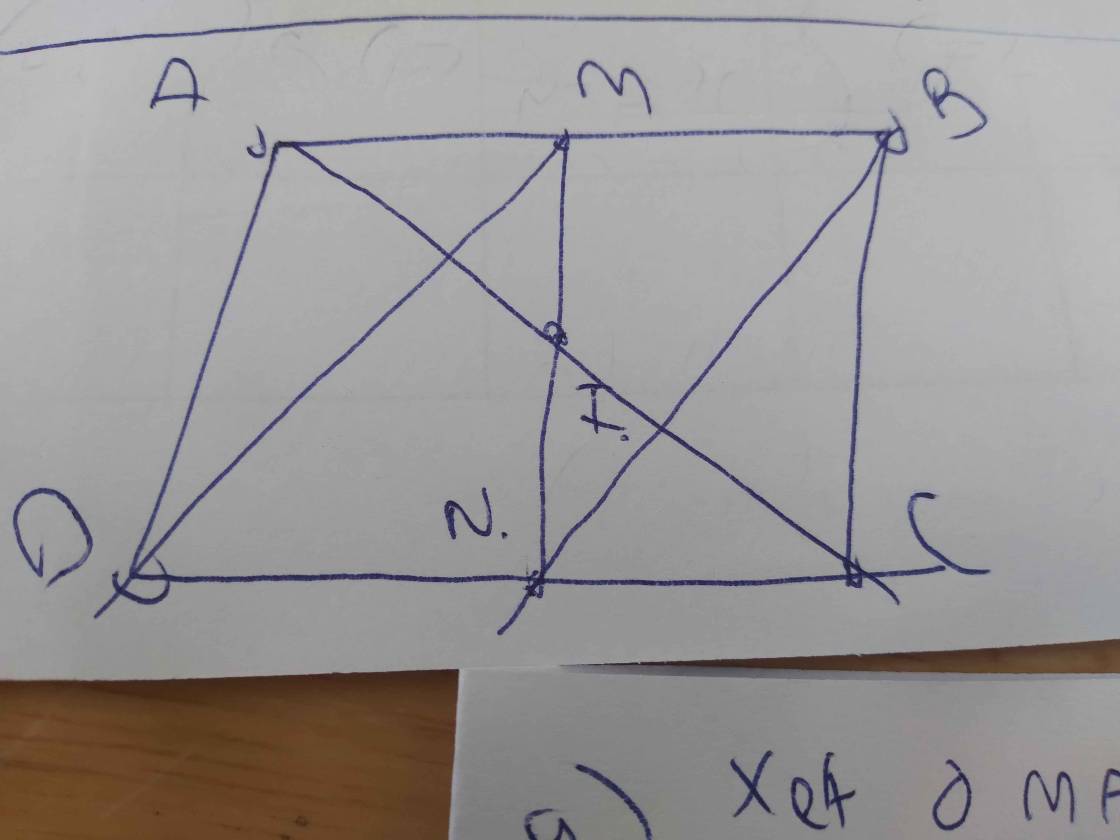
a) Do M là trung điểm của AB (gt)
⇒ BM = AM = AB : 2
Do N là trung điểm của CD (gt)
⇒ CN = DN = CD : 2
Do ABCD là hình bình hành (gt)
⇒ AB = CD và AB // CD
⇒ BM = AB : 2 = CD : 2 = DN
Do AB // CD (cmt)
⇒ BM // DN
Tứ giác BMDN có:
BM // DN (cmt)
BM = DN (cmt)
⇒ BMDN là hình bình hành
b) Do BMDN là hình bình hành (cmt)
⇒ BN // DM
⇒ ∠AMD = ∠MBN (đồng vị) (1)
Do AB // CD (cmt)
⇒ ∠MBN = ∠BNC (so le trong) (2)
Từ (1) và (2) ⇒ ∠AMD = ∠BNC
c) Do ABCD là hình bình hành
I là trung điểm của AC (gt)
⇒ I là trung điểm của BD
Do BMDN là hình bình hành (cmt)
I là trung điểm của BD (cmt)
⇒ I là trung điểm của MN
⇒ M, I, N thẳng hàng
Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: MN//AD
hay MN\(\perp\)AC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
mà MN\(\perp\)AC
nên AMCN là hình thoi
Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: MN//AD
hay MN\(\perp\)AC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
mà MN\(\perp\)AC
nên AMCN là hình thoi
a: Xét ΔAHD có
M là trung điểm của HA
N là trung điểm của HD
Do đó: MN là đường trung bình của ΔAHD
Suy ra: MN//AD
1: Xét tứ giác AMCN có
AN//CM
AN=CM
Do đó: AMCN là hình bình hành
