Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) chứng minh tứ giác AMCN là hình bình hành
M là trung điểm AB nên: AM = \(\frac{1}{2}\)BC
N là trung điểm CD nên: CN = \(\frac{1}{2}\)CD
Vì tứ giác ABCD là hình bình hành nên:
- AB = CD => AM = CN
- AB // CD => AM //CN
Tứ giác AMCN có cặp cạnh AM, CN song song và bằng nhau nên nó là hình bình hành.
b) chứng minh M, O, N thẳng hàng
* AC và BD là hai đường chéo của hình bình hành ABCD nên chúng cắt nhau tại trung điểm của mỗi đường.
Do đó, O là trung điểm AC
* AC và MN là hai đường chéo của hình bình hành AMCN nên MN phải đi qua trung điểm O của AC
hay M, O, N thẳng hàng.

M là trung điểm AB nên : \(AM=\frac{BC}{2}\)
N là trung điểm CD nên : \(CN=\frac{CD}{2}\)
Vì tứ giác ABCD là hình bình hành :
- AB = CD => AM = CN
- AB // CD => AM // CN
Tứ giác AMCN có các cặp cạnh AM , CN song song và bằng nhau nên là hình bình hành ( đpcm )
b) - AC và BD là 2 đường chéo của hình bình hành ABCD nên chúng cắt nhau tại trung điểm mỗi đường
=> O là trung điểm AC
- AC và MN là 2 đường chéo của hình bình hành AMCN nên MN phải đi qua trung điểm O của AC
hay M , O , N thẳng hàng ( đpcm )
Bài 7. Cho hình bình hành ABCD , O là giao điểm của AC và BD Gọi M và N lần lượt là trung điểm của các cạnh BC và AD . Chứng minh : a ) Tứ giác AMCN là hình bình hành . b ) Ba điểm M , O , N thẳng hàng . c ) Đường chéo BD cắt AM , CN lần lượt tại I và K. Chứng minh DK = KI = IB .

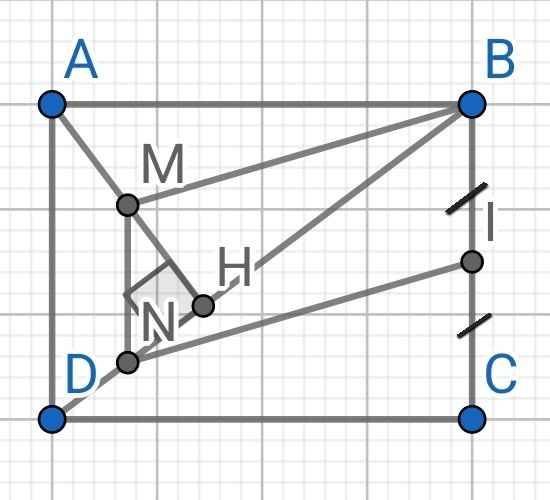 a) Do M là trung điểm AH (gt)
a) Do M là trung điểm AH (gt)
N là trung điểm DH (gt)
⇒ MN là đường trung bình của ∆ADH
⇒ MN // AD
b) Do MN // AD
⇒ MN // BC
⇒ MN // BI
Do MN là đường trung bình của ∆ADH (cmt)
⇒ MN = AD : 2 (1)
Ta có:
I là trung điểm BC (gt)
⇒ BI = BC : 2 (2)
Do ABCD là hình chữ nhật (gt)
⇒ AD = BC (3)
Từ (1), (2) và (3) ⇒ MN = BI
Tứ giác BMNI có:
MN // BI (cmt)
MN = BI (cmt)
⇒ BMNI là hình bình hành
a: Xét ΔHAD có M,N lần lượt là trung điểm của HA, HD
=>MN là đường trung bình của ΔHAD
=>MN//AD và \(MN=\dfrac{AD}{2}\)
b; MN//AD
AD//BC
Do đó: MN//BC
\(MN=\dfrac{AD}{2}\)
\(AD=BC\)
\(BI=\dfrac{BC}{2}\)
Do đó: MN=BI
Xét tứ giác MNIB có
MN//IB
MN=IB
Do đó: MNIB là hình bình hành

Giải chi tiết:
a) Xét tam giác AHD có:
M là trung điểm của AH (gt)
N là trung điểm của DH (gt)
Do đó MN là đường trung bình của tam giác AHD
Suy ra MN//AD (tính chất) (đpcm)
b) Ta có MN//AD, mà AD//BC (2 cạnh đối hình chữ nhật) nên MN//BC hay MN//BI Vì MN = 1212AD (tính chất đường trung bình của tam giác) và BI = IC = 1212BC (do gt), mà AD = BC (2 cạnh đối hình chữ nhật) MN = BI BC hay MN//BI Xét tứ giác BMNI có MN//BI, MN = BI (c/m trên) Suy ra tứ giác BMNI là hình bình hành (đpcm)
c) Ta có MN//AD và AD⊥⊥AB nên MN⊥⊥AB
Tam giác ABN có 2 đường cao là AH và NM cắt nhau tại M nên M là trực tâm của tam giác ABN. Suy ra BM⊥⊥AN.
Mà BM//IN nên AN⊥⊥NI hay ΔANIΔANI vuông tại N (đpcm)
# M̤̮èO̤̮×͜×L̤̮ườI̤̮◇

a: Xét ΔAHD có
M là trung điểm của HA
N là trung điểm của HD
Do đó: MN là đường trung bình của ΔAHD
Suy ra: MN//AD

a: Xét ΔHAD có HM/HA=HN/HD
nên MN//AD
b: Xét ΔHAD có MN//AD
nên MN/AD=HM/HA=1/2
=>MN=1/2AD=1/2BC
=>MN=BI
mà MN//BI
nên BMNI là hình bình hành

1: Xét tứ giác AMCN có
AN//CM
AN=CM
Do đó: AMCN là hình bình hành