Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) dt(ABMD) = dt(ABCD) - dt(CMD)
Mà dt(CMD) = 1/2 MC.h = 1/2 . 2/3 . BC .h = 1/3 dt(ABCD) = 1/3.S
(với h là đường cao hạ từ A xuống BC của hình bình hành ABCD)
Suy ra dt(ABMD) = S - 1/3 S = 2/3. S
b) dt(ABNT) = BN.h = 2/3 BC . h = 2/3 . S

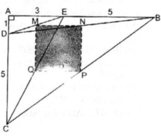
△ DMC có CM = 2/3BC
Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
S D M C = 1/2 h. 2/3 a = 1/3 ah = 1/3 S
S A B M D = S A B C D - S D M C = s - 1/3 S = 2/3 S

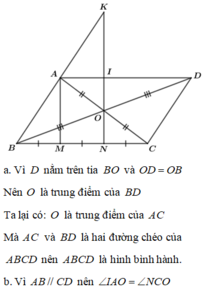
a: Xét tứ giác ABCD có
O là trung điểm chung của AC và BD
=>ABCD là hình bình hành
b: Xét ΔOAI và ΔOCN có
góc AOI=góc CON
OA=OC
góc OAI=góc OCN
=>ΔOAI=ΔOCN
=>AI=NC
=>AI=MN
mà AI//MN
nên AINM là hình bình hành
=>AM//IN


S A B C = 1/3 S A B C D = S/2
CN = 1/3 BC , NT // AB.
Theo tính chất đường thẳng song song cách đều ⇒ CT = 1/3 AC
△ ABC và △ BTC có chung chiều cao kẻ từ đỉnh B, đáy CT = 1/3 AC
⇒ S B T C = 1/3 S A B C = 1/3 . S/2 = S/6
△ BTC và △ TNC có chung chiều cao kẻ từ đỉnh T, cạnh đáy CN = 1/3 CB
⇒ S T N C = 1/3 S B T C = 1/3 . S/6 = S/18
S A B N T = S A B C - S T N C = S/2 - S/18 = 9S/18 - S/18 = 4S/9