Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Nếu HB = HC ⇒ HB2 = HC2.
⇒ AH2 + HB2 = AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 = AC2
⇒ AB = AC
- Nếu AB = AC ⇒ AB2 = AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 = AH2 + HC2
⇒ HB2 = HC2
⇒ HB = HC

AB > AC ⇒ AB2 > AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 > AH2 + HC2
⇒ HB2 > HC2
⇒ HB > HC

Xét tam giác AHB vuông tại H
Áp dụng định lí Py-ta-go ta có:
AB2 = AH2 + HB2 (1)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py-ta-go ta có:
AC2 = AH2 + HC2 (2)
Nếu HB > HC ⇒ HB2 > HC2.
⇒ AH2 + HB2 > AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 > AC2
⇒ AB > AC

`@ AB = AC`
Xét `\triangle ABH` vuông tại `H` và `\triangle ACH` vuông tại `H` có:
`{:(AB=AC),(AH\text{ là cạnh chung}):}}=>\triangle ABH =\triangle ACH` (ch+1cgv)
`=>HB=HC` (`2` cạnh t/ứ)
`@HB=HC`
Chứng mình tương tự giống trường hợp trên.

Xét ΔABC có AB<AC(gt)
mà hình chiếu của AB trên BC là HB
và hình chiếu của AC trên BC là HC
nên HC>HB

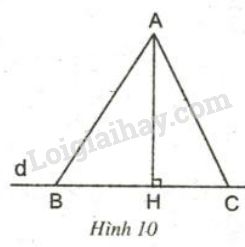
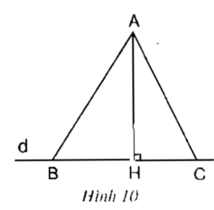
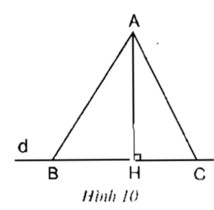
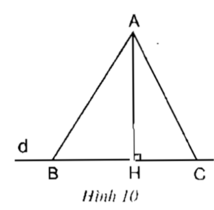
a) AB > AH; AC > AH.
b) Nếu HB > HC thì AB > AC.
hoặc có thể HB < HC thì AB < AC.
c) Nếu AB > AC thì HB > HC.
hoặc có thể AB < AC thì HB < HC.
Trả lời
a) AB > AH; AC > AH.
b) Nếu HB > HC thì AB > AC.
hoặc có thể HB < HC thì AB < AC.
c) Nếu AB > AC thì HB > HC.
hoặc có thể AB < AC thì HB < HC.

a) AB.>..AH; AC.>..AH
b) Nếu HB..>.HC thì AB.>..AC
Nếu HB..<.HC thì AB.<..AC
c) Nếu AB.<..AC thì HB.<..HC
Nếu AB.>..AC thì HB..>.HC

tròn 1 điểm:33333 chế lại làm theo định lý pytago
ta có BH^2=AB^2-AH^2( áp dụng định lý pytago)
HC^2=AC^2-AH^2( áp dụng định lý pytago)
vì AB>AC=> AB^2>AC^2=> AB^2-AH^2>AC^2-AH^2=> BH^2>HC^2 => BH>CH (BH,CH>0)
làm thêm thui chứ cách của bạn ngắn hơn và đúng:33333
TRẢ LỜI:
Xét tam giác AHB vuông tại H
Áp dụng định lí Py-ta-go ta có:
AB2 = AH2+ HB2 (1)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py-ta-go ta có:
AC2 = AH2 + HC2 (2)
Nếu HB > HC ⇒ HB2 > HC2.
⇒ AH2 + HB2 > AH2+ HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 > AC
⇒ AB > AC