Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Vì q 1 , q 3 dương nên để lực tác dụng lên q 2 bằng 0 thì F 12 ; F 23 phải cùng phương, ngược chiều và cùng độ lớn.



Hai điện tích đẩy nhau nên chúng cùng dấu; vì q 1 + q 2 < 0 nên chúng đều là điện tích âm
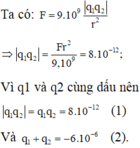
Từ (1) và (2) ta thấy q1 và q2 là nghiệm của phương trình: x 2 + 6 . 10 - 6 x + 8 . 10 - 12 = 0
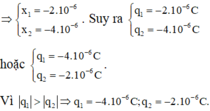

Hai điện tích đẩy nhau nên chúng cùng dấu; vì q 1 + q 2 < 0 nên chúng đều là điện tích âm.

Véc tơ lực tương tác điện giữa hai điện tích:
Ta có: F = k | q 1 q 2 | r 2 ⇒ q 1 q 2 = F r 2 k = 1 , 8.0 , 2 2 9.10 9 = 8 . 10 - 12 ;
q1 và q2 cùng dấu nên q 1 q 2 = q 1 q 2 = 8 . 10 - 12 (1) và q 1 + q 2 = - 6 . 10 - 6 (2).
Từ (1) và (2) ta thấy q 1 và q 2 là nghiệm của phương trình: x 2 + 6 . 10 - 6 x + 8 . 10 - 12 =0
⇒ x 1 = - 2 . 10 - 6 x 2 = - 4 . 10 - 6 . Kết quả q 1 = - 2 . 10 - 6 C q 2 = - 4 . 10 - 6 C hoặc x 1 = - 4 . 10 - 6 C x 2 = - 2 . 10 - 6 C
Vì q 1 > q 2 ⇒ q 1 = - 4 . 10 - 6 C ; q 2 = - 2 . 10 - 6 C .



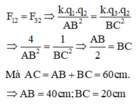
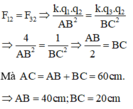
Cho hệ ba điện tích cô lập q1, q2, q3 nằm trên cùng một đường thẳng. Hai điện tích q1, q2 là hai điện tích dương, cách nhau 80 cm và q1 = 9q2. Lực điện tác dụng lên điện tích qạ bằng 0 thì điện tích qạ đặt
A. cách q1 80 cm, cách q2 20 cm.
B. cách q1 60 cm, cách q2 20 cm.
C. cách q1 20 cm, cách q2 80 cm.
D. cách q1 20 cm, cách q2 60 cm
Bài giải:
\(q_1\) và \(q_2\) cùng dấu.
Để tổng hợp lực lên \(q_3\) bằng 0
\(\Rightarrow F_{13};F_{23}\) phải ngược chiều, cùng độ lớn.
\(\Rightarrow q_3\) nằm giữa hai đoạn nối \(q_1;q_2\).
Lực do hai điện tích tác dụng lên \(q_3\):
\(\overrightarrow{F_{13}}+\overrightarrow{F_{23}}=0\Rightarrow\left|F_{13}\right|=\left|F_{23}\right|\)
Mà \(F_{13}=k\cdot\dfrac{\left|q_1\cdot q_3\right|}{r_1^2};F_{23}=k\cdot\dfrac{\left|q_2\cdot q_3\right|}{r_2^2}\)
\(\Rightarrow\dfrac{\left|q_1\right|}{r_1^2}=\dfrac{\left|q_2\right|}{r_2^2}\Rightarrow\dfrac{9}{r_1^2}=\dfrac{1}{r_2^2}\Rightarrow\dfrac{r_1}{r_2}=3\left(1\right)\)
Lại có: \(r_1+r_2=80\cdot10^{-2}=0,8\left(m\right)\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}r_1=0,6m=60cm\\r_2=0,2m=20cm\end{matrix}\right.\)
Chọn B.