Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

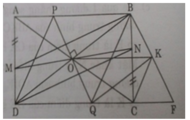
d) Gọi F là giao điểm của BK và QC. Ta có O là trung điểm của BD và OQ // BK (gt) nên Q là trung điểm của DF.
Lại có QK // BD (gt); Q là trung điểm của DF ⇒ K là trung điểm của BF.
CK là trung tuyến của tam giác vuông BCF ⇒ CK = BK = BC/2.
Ta có QK là đường trung bình của tam giác
⇒ QK = BO = BD/2; QK // BO
⇒ Tứ giác OBKQ là hình bình hành
Mặt khác ∠(OBQ) = 90o ⇒ OBKQ là hình chữ nhật
⇒ ∠(OBK) = 90o
Xét ΔOCK và ΔOBK có
CK chung
OC = OB (tính chất đường chéo hình chéo hình chữ nhật)
CK = BK (cmt)
Vậy ΔOCK = ΔOBK (c.c.c) ⇒ ∠OCK = ∠OBK = 90o hay AC ⊥ CK.

Xét \(\Delta ABC\) có
\(MP\perp AB;BC\perp AB\)=> MP//BC \(\Rightarrow\frac{AP}{PB}=\frac{AM}{MC}\) (talet trong tam giác)
Xét \(\Delta ADC\)
\(MQ\perp AD;CD\perp AD\)=> MQ//CD \(\Rightarrow\frac{AQ}{QD}=\frac{AM}{MC}\) (talet trong tam giác)
\(\Rightarrow\frac{AP}{PB}=\frac{AQ}{QD}\)
Xét \(\Delta ADB\) có
\(\frac{AP}{PB}=\frac{AQ}{QD}\) => PQ//BD (talet đảo trong tam giác)

Ý b câu hỏi là : Chứng minh EF đi qua trung điểm của AB và CD
m là 1 điểm j, viết cx sai
khổ
viết lại đi bạn
:))
tks