Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tiếp tuyến có hệ số góc bằng 1
\(y'=\dfrac{m\left(3m+1\right)-\left(-m^2+m\right)}{\left(x+m\right)^2}=\dfrac{4m^2}{\left(x+m\right)^2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\dfrac{4m^2}{\left(x+m\right)^2}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}2m=x+m\\-2m=x+m\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}x=m\\x=-3m\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\dfrac{m^2-m}{3m+1}\\-3m=\dfrac{m^2-m}{3m+1}\end{matrix}\right.\)
\(\Leftrightarrow...\)

\(\left(m^2-3m-5\right)x-y-2m+19=0\)
\(\Leftrightarrow y=\left(m^2-3m-5\right)x-2m+19\)
Ta có:
\(f'\left(x\right)=-3x^2+4x-1\)
\(f'\left(2\right)=-5\)
Phương trình tiếp tuyến tại A:
\(y=-5\left(x-2\right)+3\Leftrightarrow y=-5x+13\)
Để hai đường thẳng song song:
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-5=-5\\-2m+19\ne13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m\ne6\end{matrix}\right.\)
\(\Leftrightarrow m=0\)

Pt hoành độ giao điểm của đồ thị hàm số (C) với đường thẳng d là:
\(\dfrac{x-1}{x+1}=m-x\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\g\left(x\right)=x^2+\left(2-m\right)x-m-1=0\left(1\right)\end{matrix}\right.\)
Đồ thị (C) cắt đường thẳng d tại 2 điểm phân biệt <=> pt(1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\g\left(-1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+8>0\\-2\ne0\end{matrix}\right.\)
Khi đó: \(x_A,x_B\) là nghiệm của pt (1). Vì tiếp tuyến tại A và B //
\(\Rightarrow f'\left(x_A\right)=f'\left(x_B\right)\Leftrightarrow\dfrac{2}{\left(x_A+1\right)^2}=\dfrac{2}{\left(x_B+1\right)^2}\Leftrightarrow\left[{}\begin{matrix}x_A=x_B\left(loai\right)\\x_A+x_B=-2\end{matrix}\right.\)
Theo định lí Viet ta có:
\(x_A+x_B=m-2\Rightarrow m-2=-2\Leftrightarrow m=0\)

a:Sửa đề: y=x^3-3x^2+2
y'=3x^2-3*2x=3x^2-6x
y=2
=>x^3-3x^2=0
=>x=0 hoặc x=3
=>y'=0 hoặc y'=3*3^2-6*3=27-18=9
A(0;2); y'=0; y=2
Phương trình tiếp tuyến có dạng là;
y-2=0(x-0)
=>y=2
A(3;2); y'=9; y=2
Phương trình tiếp tuyến có dạng là:
y-2=9(x-3)
=>y=9x-27+2=9x-25
b: Tiếp tuyến tại M song song với y=6x+1
=>y'=6
=>3x^2-6x=6
=>x^2-2x=2
=>x=1+căn 3 hoặc x=1-căn 3
=>y=0 hoặc y=0
M(1+căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1-căn 3)=6x-6-6căn3
M(1-căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1+căn 3)
=>y=6x-6+6căn 3

Ủa hỏi mỗi hoành độ thôi hở :D?
\(f'\left(x\right)=2x-4\)
Vi \(pttt//d:y=8x+2017\Rightarrow f'\left(x\right)=8\)
\(\Rightarrow2x-4=8\Leftrightarrow x=6\)
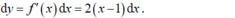

Các điều kiện về xác định coi như thỏa mãn
\(y'=\frac{\left(3m+1\right)m-1\left(-m^2+m\right)}{\left(x+m\right)^2}=\frac{4m^2}{\left(x+m\right)^2}\)
Giao điểm của (C) với trục hoành thỏa mãn: \(\left(3m+1\right)x=m^2+m\Rightarrow x=\frac{m^2+m}{3m+1}\)
Do tiếp tuyến song song d
\(\Rightarrow y'\left(\frac{m^2+m}{3m+1}\right)=1\Rightarrow\left[{}\begin{matrix}\frac{2m}{\frac{m^2+m}{3m+1}+1}=1\\\frac{2m}{\frac{m^2+m}{3m+1}+1}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2m=\frac{m^2+m}{3m+1}+1\\2m=-\frac{m^2+m}{3m+1}-1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}5m^2-2m-1=0\\7m^2+6m+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\frac{1\pm\sqrt{6}}{5}\\m=\frac{-3\pm\sqrt{2}}{7}\end{matrix}\right.\)
Bạn kiểm tra lại tính toán