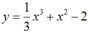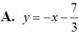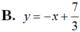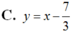Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm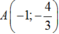 
là: y = -1.(x + 1) - 7/3
Hay 
.
\(f'\left(x\right)=2x-2\)
a/ \(f'\left(1\right)=0\) ; \(f\left(1\right)=2\)
Phương trình tiếp tuyến: \(y=2\)
b/ \(4x-2y+5=0\Leftrightarrow y=2x+\frac{5}{2}\)
Tiếp tuyến song song d nên có hệ số góc bằng 2
\(\Rightarrow2x_0-2=2\Rightarrow x_0=2\)
\(f\left(2\right)=3\)
Pt tiếp tuyến: \(y=2\left(x-2\right)+3=0\Leftrightarrow y=2x-1\)
c/ \(x+4y=0\Rightarrow y=-\frac{1}{4}x\)
Tiếp tuyến vuông góc d \(\Rightarrow\) có hsg k thỏa mãn \(k.\left(-\frac{1}{4}\right)=-1\Rightarrow k=4\)
\(\Rightarrow2x_0-2=4\Rightarrow x_0=3\) ; \(f\left(3\right)=6\)
Pt tiếp tuyến: \(y=3\left(x-3\right)+6=3x-3\)
d/ Đường phân giác góc phần thứ thứ nhất có pt \(y=x\)
\(\Rightarrow\) Tiếp tuyến có hệ số góc -1
\(\Rightarrow2x_0-2=-1\Rightarrow x_0=\frac{1}{2}\) ; \(f\left(\frac{1}{2}\right)=\frac{9}{4}\)
Pt: \(y=-1\left(x-\frac{1}{2}\right)+\frac{9}{4}=-x+\frac{11}{4}\)
Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
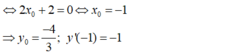
- Phương trình tiếp tuyến tại điểm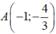 
là:
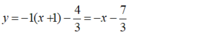
Chọn A.
- Ta có :
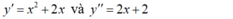
- Theo giả thiết x 0 là nghiệm của phương trình:
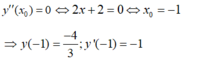
- Phương trình tiếp tuyến tại điểm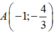 
là:
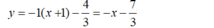
Chọn A.
- Gọi d là tiếp tuyến của đồ thị hàm số đã cho qua A( 0, 2)
→ phương trình của d có dạng: y = k(x - 0) + 2 hay y = kx + 2
- Vì d tiếp xúc với đồ thị (C) nên hệ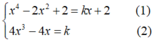
có nghiệm.
- Thay (2) vào (1) ta được :
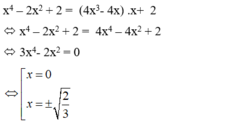
- Tương ứng với ba giá trị của x ta vừa tìm được, ta viết được 3 tiếp tuyến đi qua Ađến đồ thị (C).
Chọn B.
Câu 1:
\(ABCI\) là hình vuông \(\Rightarrow\left\{{}\begin{matrix}CD=\sqrt{IC^2+ID^2}=a\sqrt{2}\\AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow AC^2+CD^2=AD^2\Rightarrow\Delta ACD\) vuông cân tạiC
\(\Rightarrow OC\perp CD\) \(\Rightarrow CD\perp\left(SOC\right)\)
Từ O kẻ \(OH\perp SC\Rightarrow OH\perp\left(SCD\right)\) \(\Rightarrow OH\perp SD\)
\(\left\{{}\begin{matrix}BI\perp SO\\BI\perp OC\end{matrix}\right.\) \(\Rightarrow BI\perp\left(SOC\right)\Rightarrow BI\perp OH\)
\(SC=\sqrt{SO^2+OC^2}=a\sqrt{2}\) \(\Rightarrow SH=\frac{SO^2}{SC}=\frac{3a\sqrt{2}}{4}\)
Qua H kẻ đường thẳng song song CD cắt SD tại K
\(\frac{SH}{SC}=\frac{HK}{CD}\Rightarrow HK=\frac{SH.CD}{SC}=\frac{3a}{4}\)
Trên toa OI lấy điểm P sao cho \(OP=\frac{3a}{4}\)
\(\Rightarrow OHKP\) là hình chữ nhật \(\Rightarrow OH//KP\Rightarrow KP\) là đoạn vuông góc chung của \(BI\) và SD
\(\frac{1}{OH^2}=\frac{1}{SO^2}+\frac{1}{OC^2}\Rightarrow KP=OH=\frac{SO.OC}{\sqrt{SO^2+OC^2}}=\frac{a\sqrt{6}}{4}\)
Câu 2:
a/ Kẻ \(MH\perp AC\Rightarrow MH\perp\left(SAC\right)\)
\(\Rightarrow\widehat{MSH}\) là góc giữa SM và (SAC)
\(SM=\sqrt{SA^2+\left(\frac{AB}{2}\right)^2}=a\sqrt{10}\) ; \(MH=\frac{1}{2}\frac{2a\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}\)
\(sin\widehat{MSH}=\frac{MH}{SM}=\frac{\sqrt{30}}{20}\Rightarrow\widehat{MSH}\approx15^053'\)
b/ \(\left\{{}\begin{matrix}MC\perp AB\\MC\perp SA\end{matrix}\right.\) \(\Rightarrow MC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{SMA}\) là góc giữa \(\left(SMC\right)\) và \(\left(ABC\right)\)
\(tan\widehat{SMA}=\frac{SA}{AM}=3\Rightarrow\widehat{SMA}\approx71^033'\)
c/ Gọi N là trung điểm AC \(\Rightarrow NG=\frac{1}{3}NS\) (t/c trọng tâm)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\frac{1}{3}d\left(N;\left(SAB\right)\right)\)
Từ N kẻ \(NK\perp AB\Rightarrow NK\perp\left(SAB\right)\)
\(\Rightarrow NK=d\left(N;\left(SAB\right)\right)\)
\(NK=\frac{1}{2}.\frac{2a\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}\Rightarrow d\left(G;\left(SAB\right)\right)=\frac{a\sqrt{3}}{6}\)