Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có: y’ = 8x3 – 8x
ð y’ = 0 ó x = 0 hoặc x = 1 hoặc x = -1
Ta có bảng biến thiên:
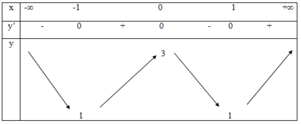
Vậy các điểm cực trị của hàm là: (-1;1), (0;3) và (1;1)
Theo công thức tính diện tích tam giác, ta có:
S = p ( p − a ) ( p − b ) ( p − c )
Trong đó
p = a + b + c 2
Vậy diện tích tam giác tạo bởi 3 điểm cực trị của đồ thị hàm số là 2

Đáp án D
Có f ' x = 8 x 3 − 8 x ; f ' x = 0 ⇔ x = 0 x = 1 x = − 1
Từ đó 3 điểm cực trị là A − 1 ; 1 ; B 0 ; 3 ; C 1 ; 1 .
Nhận thấy rằng A B C là tam giác cân tại B với đường cao là BM , M là trung điểm của AC.
Tinh được A C = 2 ; B M = 2 ⇒ S A B C = 1 2 .2.2 = 2 .

Đáp án D
Ta có: y = f ' x = 4 x 3 − 4 x = 4 x x 2 − 1 ⇔ x = 0 x = ± 1
=> Các điểm cực trị là A 0 ; 3 , B 1 ; 2 , C − 1 ; 2 ⇒ Δ A B C cân tại
A ; B C = 1 + 1 2 + 2 − 2 2 = 2
Gọi I là trung điểm của B C ⇒ I 0 ; 2 ⇒ A I = h = 1
Ta có: S = 1 2 A I . B C = 1
Cách 2: Áp dụng CT giải nhanh: S = b 2 4 a . − b 2 a = 1

Đáp án D
Ta có
y ' = 4 x 3 − 4 x = 0 ⇔ x = 0 ⇒ y = 3 ⇒ A 0 ; 3 x = ± 1 ⇒ y = 2 ⇒ B 1 ; 2 , C − 1 ; 2
⇒ A B → = − 2 ; 0 ⇒ B C = 2 B C : y = 2 ⇒ d A ; B C = 1 ⇒ S A B C = 1 2 B C . d A ; B C = 1

Đáp án B
Sai lầm thường gặp: Tập xác định D = ℝ \ 3 .
Đạo hàm y ' = − 2 x − 3 2 ,0, ∀ x ∈ D ⇒ Hàm số nghịch biến trên ℝ \ 3 , hoặc làm số nghịch biến trên − ∞ ; 3 ∪ 3 ; + ∞ . Hàm số không có cực trị.
Tiệm cận đứng: x=3; tiệm cận ngang: y=1. Đồ thị hàm số nhận giao điểm I 3 ; 1 của hai đường tiệm cận làm tâm đối xứng.
Từ đó nhiều học sinh kết luận các mệnh đề 1 , 3 , 4 đúng và chọn ngay A.
Tuy nhiên đây là phương án sai.
Phân tích sai lầm:
Mệnh đề (1) sai, sửa lại: hàm số nghịch biến trên mỗi khoảng − ∞ ; 3 và 3 ; + ∞ . Học sinh cần nhớ rằng, ta chỉ học định nghĩa hàm số đồng biến (nghịch biến) trên khoảng, đoạn, nửa khoảng; chứ không có trên những khoảng hợp nhau.
Mệnh đề (2) sai. Đồ thị hàm số có một tiệm cận đứng là x=3, một tiệm cận ngang là y=1.
Mệnh đề 3 , 4 đúng.
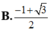
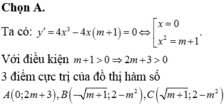


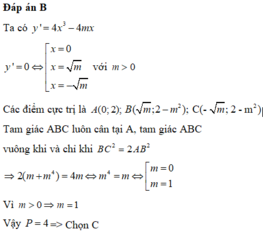

Đáp án C
Ta có y ' = 4 x 3 − 4 x ; y ' = 0 ⇔ x = 0 ⇒ y 0 = 2 x = ± 1 ⇒ y ± 1 = 1
Suy ra 3 điểm cực trị của ĐTHS là A 0 ; 2 , B 1 ; 1 , C − 1 ; 1
Khi đó A B = A C = 2 , B C = 2 ⇒ S Δ A B C = 1 2 A B 2 = 2 2 2 = 1