Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.

Mệnh đề 3 sai ví dụ hàm số y=|x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó.
Mệnh đề 4 đúng vì nếu hàm số y=f(x) có đạo hàm trên [a;b] thì hàm số liên tục trên [a;b] do đó hàm số có nguyên hàm trên [a;b]

Đáp án B
Đặt t = a − x ⇒ d t = − d x
và x = 0 x = a → t = a t = 0
I = ∫ 0 a d x 1 + f x = ∫ 0 a d x 1 + f a − t = ∫ 0 a d x 1 + 1 f x = ∫ 0 a f x d x 1 + f x
⇒ 2 I = ∫ 0 a d x 1 + f x + ∫ 0 a f x d x 1 + f x = ∫ 0 a d x = x a 0 = a ⇒ I = a 2 = b a 2 ⇒ b = 1 c = 2 ⇒ b + c = 3

Đáp án A.
Ta có
F x = ∫ 3 x 2 + 1 2 x + 1 d x = x 3 + 1 2 ln 2 x + 1 + C
mà F 0 = 0 ⇒ C = 0
Do đó
F x = x 3 + 1 2 ln 2 x + 1 ⇒ F 1 = 1 + 1 2 ln 3 ⇒ a = 1 ; b = 1 ; c = 2 ⇒ a + b + c = 4 .






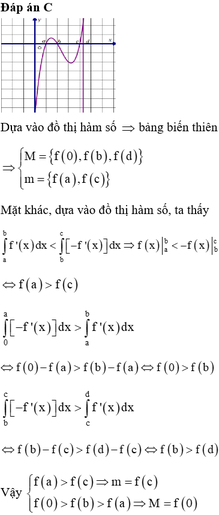
Đáp án B