Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ đồ thị hàm số y = x2.
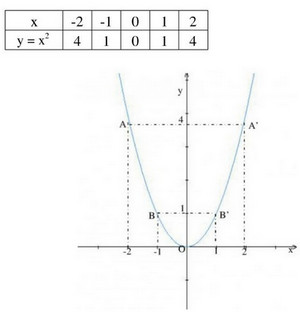
b) Ta có y = f(x) = x2 nên
f(-8) = (-8)2 = 64; f(-1,3) = (-1,3)2 = 1,69; f(-0,75) = (-0,75)2 = 0,5625; f(1,5) = 1,52 = 2,25.
c) Theo đồ thị ta có:
(0,5)2 ≈ 0,25
(-1,5)2 ≈ 2,25
(2,5)2 ≈ 6,25
d) Theo đồ thị ta có: Điểm trên trục hoành √3 thì có tung độ là y = (√3)2 = 3. Suy ra điểm biểu diễn √3 trên trục hoành bằng 1,7. Tương tự điểm biểu diễn √7 gồm bằng 2,7.

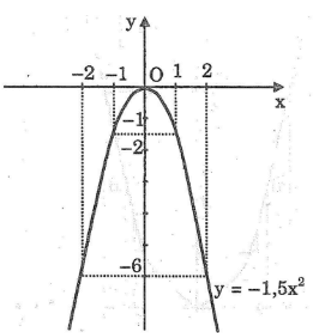
a:
b: Vì a=-1,5<0 nên hàm số đồng biến khi x<0 và nghịch biến khi x>0
=>f(-1,5)< f(-0,5) và f(0,75)>f(1,5)
- Khi 1 ≤ x ≤ 2 thì -6 ≤ y ≤ -1,5 ;
- Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0 ;
- Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0.

a) f(5) = 2; f(1) = 0; f(0) không tồn tại; f(-1) không tồn tại.
b) Để hàm số được xác định thì \(x-1\ge0\Leftrightarrow x\ge1\)
c) Gọi x0 là số bất kì thỏa mãn \(x\ge1\). Khi đó ta có:
\(h\left(x_0\right)=f\left[\left(x_0+1\right)-1\right]-f\left(x_0-1\right)=\sqrt{x_0}-\sqrt{x_0-1}\)
\(h\left(x_0\right)\left[f\left(x_0+1\right)+f\left(x_0\right)\right]=\left(\sqrt{x_0}-\sqrt{x_0-1}\right)\left(\sqrt{x_0}+\sqrt{x_0-1}\right)=x_0-\left(x_0-1\right)=1>0\)
Vì \(\sqrt{x_0}+\sqrt{x_0-1}>0\Rightarrow h\left(x_0\right)>0\)
Vậy thì với các giá trị \(x\ge1\) thì hàm số đồng biến.

a: f(1)=-1,5
f(2)=-6
f(3)=-13,5
=>f(1)>f(2)>f(3)
b: \(f\left(-3\right)=-1,5\cdot9=-13,5\)
f(-2)=-1,5x4=-6
f(-1)=-1,5x1=-1,5
=>f(-3)<f(-2)<f(-1)
c: Hàm số này đồng biến khi x<0 và nghịch biến khi x>0

bạn ấn vào đúng 0 sẽ ra kết quả, mình giải được rồi dễ lắm

Ta có \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\)
Xét với x = a thì ta có \(f\left(a\right)+2f\left(\frac{1}{a}\right)=a^2\) (1)
Xét với x = \(\frac{1}{a}\) thì ta có \(f\left(\frac{1}{a}\right)+2f\left(a\right)=\frac{1}{a^2}\)(2)
Từ (1) và (2) ta suy ra \(\hept{\begin{cases}f\left(a\right)+2f\left(\frac{1}{a}\right)=a^2\\f\left(\frac{1}{a}\right)+2f\left(a\right)=\frac{1}{a^2}\end{cases}\Leftrightarrow}\hept{\begin{cases}f\left(a\right)+2f\left(\frac{1}{a}\right)=a^2\left(1\right)\\2f\left(\frac{1}{a}\right)+4f\left(a\right)=\frac{2}{a^2}\left(2\right)\end{cases}}\)
Lấy (2) trừ (1) theo vế được \(3f\left(a\right)=\frac{2}{a^2}-a^2\Leftrightarrow f\left(a\right)=\frac{\frac{2}{a^2}-a^2}{3}=\frac{2-a^4}{3a^2}\)
Từ đó suy ra được \(f\left(x\right)=\frac{2-x^4}{3x^2}\)
Đến đây dễ dàng tính được f(2)
Mình kí hiệu (1) (2) hai lần , bạn sửa lại chỗ đó nhé ^^

Từ x1 < x2 và 3 > 0
suy ra : 3x1< 3x2 hay f(x1) < f(x2 ).
Vậy hàm số đã cho đồng biến trên R.
f(-8) = (-8)2 = 64
f(-1,3) = (-1,3)2 = 1,69
f(-0,75) = (-0,75)2 = 0,5625
f(1,5) = (1,5)2 = 2,25.