Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)

Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

a.f(-2)=/2.(-2)-3/=/-4-3/=/-7/=7
f(8)=/2.8-3/=/16-3/=/13/=13
b. với y =-1 ta có: /2x-3/=-1(vô nghiệm)
với y=3 ta có: /2x-3/=3
2x-3=3 hoặc 2x-3=-3
2x=6 hoặc 2x=0
x=3 hoặc x=0
a) Ta lần lượt có :
f ( - 2 ) = | 2-(-2)-3 | = | -4 - 3 | = | -7 | = 7
f( 8 ) = | 2x - 3 | = | 2 . 8 - 3 | = | 16 - 3 | = | 13 | = 13
b) Ta lần lượt có :
- Với y = -1 thì | 2x - 3 | = -1 , vô nghiệm bởi | 2x - 3 | > 0
- Với y = 3 thì | 2x - 3 | = 3
↔ 2x - 3 = 3 hoặc 2x - 3 = -3
↔ 2x = 6 hoặc 2x = 0
↔ x = 3 hoặc x = 0

1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)
b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5
Thay y=5 và x=0 vào hs và tìm k
2. a) Tự vẽ
b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)
c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y) (x=-2; y=0)
3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)
Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1
Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3

a) Ta có:
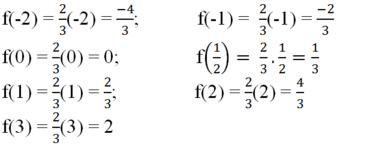
b) Ta có:
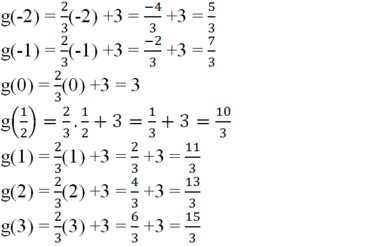
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
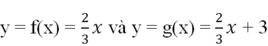
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.

a) Ta có bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 4 |
Vẽ đồ thị hàm số :
Trên hệ trục tọa độ xác định các điểm (-2 ; 4) ; (-1 ; 1) ; (0 ; 0) ; (1 ; 1) ; (2 ; 4). Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = x 2 .
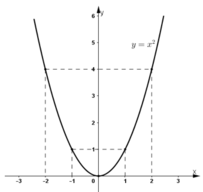
c)
– Để ước lượng giá trị ( 0 , 5 ) 2 ta tìm điểm A thuộc đồ thị có hoành độ là 0,5. Khi đó, tung độ của điểm A chính là giá trị ( 0 , 5 ) 2 . Từ điểm (0,5;0) trên trục hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm A. Từ điểm A trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của ( 0 , 5 ) 2
– Để ước lượng giá trị ( - 1 , 5 ) 2 ta tìm điểm B thuộc đồ thị có hoành độ là -1,5. Khi đó, tung độ của điểm B chính là giá trị ( - 1 , 5 ) 2 . Từ điểm (-1,5;0) trên trục hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm B. Từ điểm B trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của ( - 1 , 5 ) 2
– Để ước lượng giá trị ( 2 , 5 ) 2 ta tìm điểm C thuộc đồ thị có hoành độ là 2,5. Khi đó, tung độ của điểm C chính là giá trị ( 2 , 5 ) 2 . Từ điểm (2,5;0) trên trục hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm C. Từ điểm C trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của ( 2 , 5 ) 2
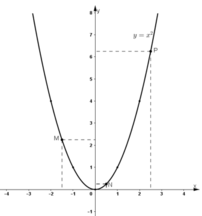
Trên đồ thị hàm số, lấy các điểm M, N, P có hoành độ lần lượt bằng -1,5 ; 0,5 và 2,5.
Dựa vào đồ thị nhận thấy các điểm M, N, P có tọa độ là : M(-1,5 ; 2,25) ; N(0,5 ; 0,25) ; P(2,5 ; 6,25).
Vậy ( 0 , 5 ) 2 = 2 , 25 ; ( - 1 , 5 ) 2 = 2 , 25 ; ( 2 , 5 ) 2 = 6 , 25 .
d)
– Để ước lượng vị trí điểm biểu diễn số √3 trên trục hoành ta tìm điểm M thuộc đồ thị có tung độ là ( √ 3 ) 2 = 3 . Khi đó, hoành độ của điểm M chính là vị trí điểm biểu diễn √3. Từ điểm (0;3) trên trục tung ta kẻ đường thẳng song song với Ox cắt đồ thị tại điểm M. Từ điểm M trên đồ thị kẻ đường thẳng song song với Oy ta xác định được hoành độ của điểm M chính là vị trí điểm biểu diễn √3
– Để ước lượng vị trí điểm biểu diễn số √7 trên trục hoành ta tìm điểm N thuộc đồ thị có tung độ là ( √ 7 ) 2 = 7 . Khi đó, hoành độ của điểm N chính là vị trí điểm biểu diễn √7. Từ điểm (0;7) trên trục tung ta kẻ đường thẳng song song với Ox cắt đồ thị tại điểm N. Từ điểm N trên đồ thị kẻ đường thẳng song song với Oy ta xác định được hoành độ của điểm N chính là vị trí điểm biểu diễn √7
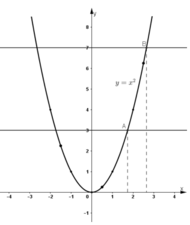
Ta có : ( √ 3 ) 2 = 3 ; ( √ 7 ) 2 = 7
⇒ Các điểm (√3 ; 3) và (√7 ; 7) thuộc đồ thị hàm số y = x 2
Để xác định các điểm √3 ; √7 trên trục hoành, ta lấy trên đồ thị hàm số các điểm A, B có tung độ lần lượt là 3 và 7.
Chiếu vuông góc các điểm A, B trên trục hoành ta được các điểm √3 ; √7 trên đồ thị hàm số.

a) Hàm số đồng biến nếu \(\dfrac{k^2+2}{k-3}>0\) \(\Leftrightarrow k>3\)
b) Hàm số nghịch biến nếu \(\dfrac{k+\sqrt{2}}{k^2+\sqrt{3}}< 0\Leftrightarrow k< -\sqrt{2}\)

1: Khi m=3/2 thì \(\left(d\right):y=\left(2\cdot\dfrac{3}{2}-1\right)x+3=2x+3\)
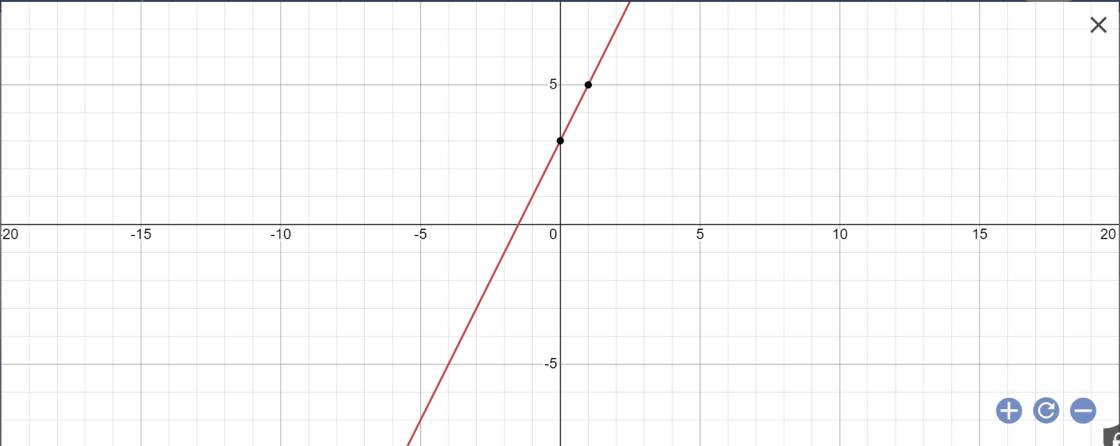
2: \(tanx=a=2m-1\)
3:
Để hai đồ thị (d) và (d') song song với nhau thì:
\(2m-1=3\)
=>2m=4
=>m=2
4: Thay x=1 vào (d1), ta được:
\(y=2\cdot1-3=-1\)
Thay x=1 và y=-1 vào (d), ta được:
\(1\left(2m-1\right)+3=-1\)
=>2m+2=-1
=>2m=-3
=>\(m=-\dfrac{3}{2}\)
5: y=1
=>2x-3=1
=>2x=4
=>x=2
Thay x=2 và y=1 vào (d),ta được:
\(2\left(2m-1\right)+3=1\)
=>2(2m-1)=-2
=>2m-1=-1
=>2m=0
=>m=0
Đáp án là C