Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

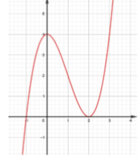
Chọn A
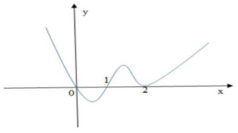
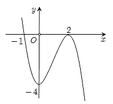
Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực đại tại x = 0, hàm số đạt cực tiểu tại x = 2.
Vậy đồ thị hàm số có 2 điểm cực trị.
Chọn D

Chọn A.
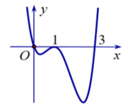
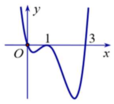
Theo đồ thị ta có: f'(x) > 0 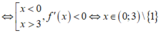
Ta có: ![]()
Cho y' = 0
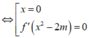
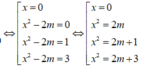
Để hàm số có 3 điểm cực trị thì phương trình y' = 0 phải có 3 nghiệm bội lẻ
Ta thấy x = 0 là một nghiệm bội lẻ
Dựa vào đồ thị của y = f'(x) ta thấy x = 1 là nghiệm bội lẻ (không đổi dấu), do đó ta không xét trường hợp ![]()
Suy ra để hàm số có 3 điểm cực trị thì
TH1: x 2 = 2m có 2 nghiệm phân biệt khác 0 và x 2 = 2m + 3 vô nghiệm hoặc có nghiệm kép bằng 0
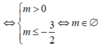
TH2. x 2 = 2m + 3 có 2 nghiệm phân biệt khác 0 và x 2 = 2m vô nghiệm hoặc có nghiệm kép bằng 0
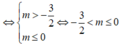
Vậy hàm số của 3 điểm cực trị khi 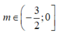

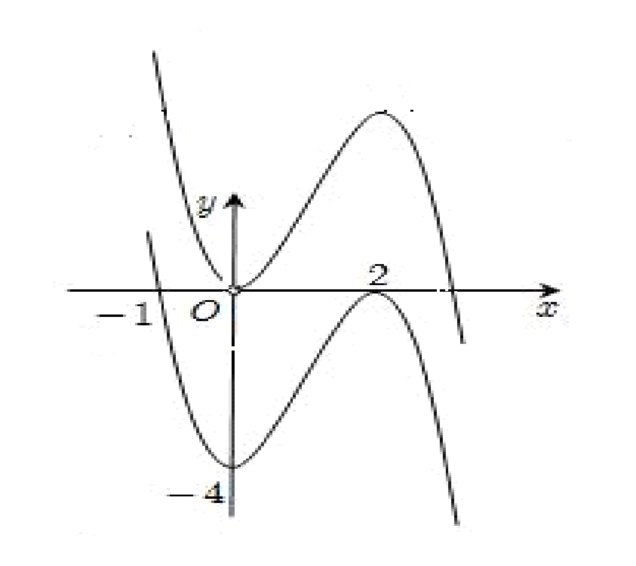
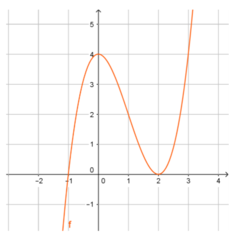
+Ta có đạo hàm f’ (x)= 3ax2+ 2bx+c .
+ Dựa vào đồ thị hàm số y= f’ ( x) ta thấy đồ thị hàm số đi qua các điểm (0 ; 0) ; (1 ; -1) ; (2 ; 0) nên a= 1/3 ; b= -1 ; c= 0.
Do vậy hàm số cần tìm có dạng y= 1/3 x3-x2+ d .
Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x= 0 hoặc x= 2. + Vì đồ thị hàm số y= f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm x= 2 nghĩa là:
f( 2) = 0 hay 8/3-4+ d= 0 nên d= 4/3
Chọn D.

Chọn A
Ta có: ![]() có đồ thị là phép tịnh tiến đồ thị hàm số y= f’(x) theo phương Oy lên trên 4 đơn vị.
có đồ thị là phép tịnh tiến đồ thị hàm số y= f’(x) theo phương Oy lên trên 4 đơn vị.
Khi đó đồ thị hàm số y= f( x) + 4x cắt trục hoành tại 1 điểm.
ta chọn đáp án A.

Chọn C
Đồ thị hàm số y= f’( x+ 2018) là phép tịnh tiến của đồ thị hàm số y= f’(x) song song với trục hoành về bên trái 2018 đơn vị.
=> đồ thị hàm số y= f’( x+ 1018) vẫn cắt trục hoành tại 3 điểm.
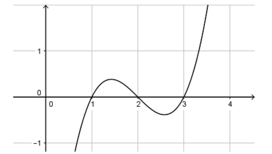
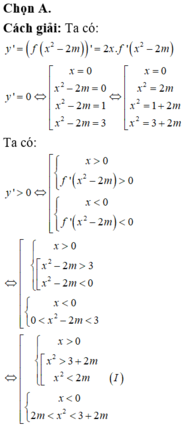
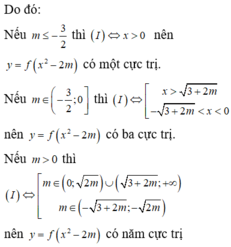

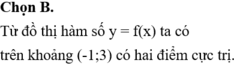

Chọn C