Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
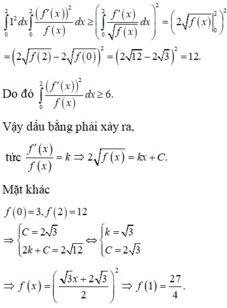
Đáp án A

Chọn D
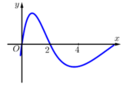
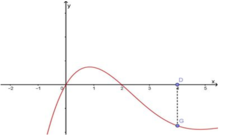
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
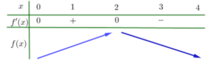
Từ bảng biến thiên, ta có nhận xét sau: ![]()
![]()
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
![]()
![]()
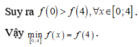

Chọn B
Ta có:
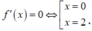
biến thiên của hàm số f(x) trên đoạn [0;4]
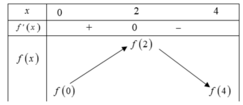
Nhìn vào bảng biến thiên ta thấy ![]()
Ta có f(2) + f(4) = f(3) + f(0) ⇔ f(0) - f(4) = f(2) - f(3) > 0.
Suy ra: f(4) < f(0). Do đó ![]()
Vậy giá trị nhỏ nhất và lớn nhất của f(x) trên đoạn [0;4] lần lượt là: f(4), f(2).

Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
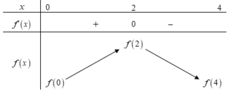
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)

Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
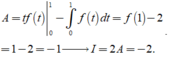

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
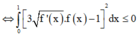
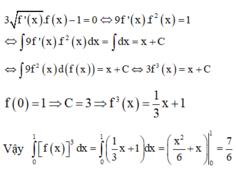

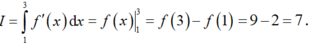
Xét hàm f x = 3 x 2 + 6 x 2 + 6 x + 1 3 trên - 2 ; 1
Ta có
Nhận thấy f ' x > 0 , ∀ x ∈ ℝ
⇒ Hàm số đồng biến trên - 2 ; 1
Suy ra m a x [ - 2 , 1 ] f x = f 1 = 16 3
Chọn C