Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Để $\left\{x\in\mathbb{R}|x^2-mx+n=0\right\}=\left\{1;2\right\}$ thì $x^2-mx+n=0$ có nghiệm $x=1$ và $x=2$Điều này xảy ra khi:
\(\left\{\begin{matrix} 1-m+n=0\\ 4-2m+n=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m=3\\ n=2\end{matrix}\right.\)
2.
Để $\left\{x\in\mathbb{R}|x^3-mx^2+nx-2=0\right\}=\left\{1;2\right\}$ thì pt $x^3-mx^2+nx-2=0$ chỉ có 2 nghiệm $x=1$ và $x=2$Điều này xảy ra khi:
$x^3-mx^2+nx-2=(x-1)^2(x-2)$ (chọn) hoặc $x^3-mx^2+nx-2=(x-1)(x-2)^2$ (loại)
$\Leftrightarrow x^3-mx^2+nx-2=x^3-4x^2+5x-2$
$\Rightarrow m=4; n=5$

Dễ thấy: \(f\left(x\right)=\left(x+m-1\right)^2-m^2+5m-6\ge-m^2+5m-6\)
Giá trị nhỏ nhất của f(x) đạt lớn nhất tức \(-m^2+5m-6\) đạt lớn nhất
Mà \(g\left(m\right)=-m^2+5m-6=-\left(m-\dfrac{5}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
g(m) đạt lớn nhất khi m=5/2
m cần tìm là 5/2

a) ta có \(\Delta=\left(-m\right)^2-4\left(-1\right)1=m^2+4\ge4>0\forall m\)
\(\Rightarrow\) phương trình luôn có 2 nghiệm phân biệt (đpcm)
bài này nếu ai lanh sẽ thấy hệ số \(a\) và \(c\) trái dấu nên \(\Rightarrow\) (đpcm) luôn ; không cần trình bày dài dòng .
b) vì phương trình đã luôn có 2 nghiệm phân biệt rồi nên không cần tìm điện kiện để phương trình có 2 nghiệm phân biệt nữa .
áp dụng hệ thức vi - ét ta có : \(\left\{{}\begin{matrix}x_1x_2=-1\\x_1+x_2=-m\end{matrix}\right.\)
ta có : \(x_1^2+x_2^2=5\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5\)
\(\Leftrightarrow\left(-m\right)^2-2\left(-1\right)=m^2+2=5\) \(\Leftrightarrow m^2=3\Leftrightarrow m=\pm\sqrt{3}\)
vậy \(m=-\sqrt{3};m=\sqrt{3}\)

Phương trình có hai nghiệm
![]()
B = 2 ( x 1 2 + x 2 2 ) + 16 − 3 x 1 x 2
= 2 ( x 1 + x 2 ) 2 − 4 x 1 x 2 + 16 − 3 x 1 x 2 = 2 ( 2 m + 2 ) 2 − 4 ( m 2 + 2 ) + 16 − 3 ( m 2 + 2 ) = 4 m 2 + 16 m + 16 − 3 ( m 2 + 2 ) = 2 m + 4 − 3 ( m 2 + 2 ) = − 3 m 2 + 2 m − 2
Xét hàm số y = − 3 m 2 + 2 m − 2 với m ≥ 1 2
Bảng biến thiên
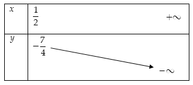
Suy ra giá trị m a x m ≥ 1 2 y = − 7 4 khi m = 1 2
Vậy giá trị lớn nhất của biểu thức B là - 7 4 khi m = 1 2
Đáp án cần chọn là: B

Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2

Tọa độ I là: \(I\left(\dfrac{3}{2};-\dfrac{1}{4}\right)\)
Phương trình \(d_m\): \(m\left(x-2\right)-y+1=0\)
\(\Rightarrow d_m\) luôn đi qua điểm cố định \(A\left(2;1\right)\)
Gọi H là hình chiếu vuông góc của I lên \(d_m\) \(\Rightarrow IH=d\left(I;d_m\right)\)
\(\Rightarrow IH\le IA\) (theo định lý đường xiên - đường vuông góc)
\(\Rightarrow IH_{max}=IA\) khi H trùng A hay \(d_m\) nhận \(\overrightarrow{IA}=\left(\dfrac{1}{2};\dfrac{5}{4}\right)=\dfrac{1}{4}\left(2;5\right)\) là 1 vtpt
\(\Rightarrow\dfrac{m}{2}=\dfrac{-1}{5}\Rightarrow m=-\dfrac{2}{5}\)

Thầy ơi con đang làm theo hướng này thì giải tiếp như thế nào vậy ạ?